Криволинейный интеграл 2-го рода (криволинейный интеграл по координатам). Формула Грина. Примеры решения задач по высшей математике онлайн

Ничего страшного в этом заголовке нет – по существу, мы продолжаем решать криволинейные интегралы 2-го рода

формула Грина – Остроградского

Или, как её чаще называют – просто формула Грина, которую обычно записывают для положительного направления обхода контура:
, где  – замкнутая область, ограниченная контуром .

Примечание: функции  должны быть определены и непрерывны в области

Решим наш интеграл  по формуле Грина. Сначала найдём частные производные:

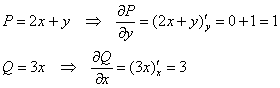
И, выбирая привычный порядок обхода области , получаем:

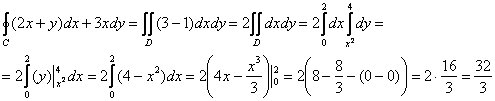
Как видите, решение сильно сократилось, а иногда оно сокращается просто фантастически!

Пример 11

Вычислить криволинейный интеграл  по окружности :
а) непосредственно, б) по формуле Грина.

Решение: естественно, здесь не нужно мучиться с дугами  (хотя можно) – гораздо проще представить уравнение окружности  в параметрической форме, которая уже неоднократно встречалась ранее:

В условии ничего не сказано о направлении обхода контура, но пункт «бэ» толсто намекает, что лучше двигаться против часовой стрелки. К тому же, традиционное возрастание параметра  как раз и обеспечивает «виток» именно в этом направлении:

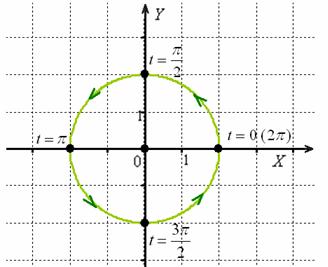
Чертёж, к слову, был вовсе не обязателен, и ввиду простоты контура можно было обойтись и без него. Однако не в этот раз – пожалуйста, ХОРОШО запечатлите эту картинку в своём сознании!

а) Вычислим криволинейный интеграл непосредственно. Алгоритм решения обычный – «начинку» интеграла нужно «заправить» буквой «тэ». Найдём дифференциалы:

и подставим  в подынтегральное выражение. Чтобы не запутаться рекомендую оформлять преобразования «простынёй»:

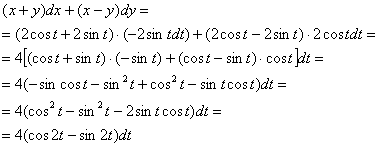
…надеюсь, использованные тригонометрические формулы вы не забудете в любом состоянии =) 

Таким образом, криволинейный интеграл:

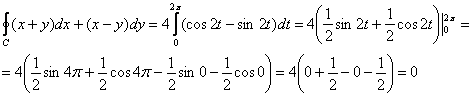
б) Вычислим интеграл по формуле Грина:
, где  – замкнутая область, ограниченная контуром . В данном случае это круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку:

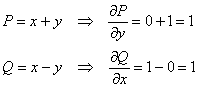
и сбылась мечта тунеядца:)

Ответ:

И это не только приятный, но ещё и крайне интересный случай. Если криволинейный интеграл по замкнутому контуру равен нулю, то речь заходит об очень крутом свойстве! Рассмотрим две произвольные точки области . Очевидно, что их можно соединить бесчисленным количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же значению!

Вернёмся к только что разобранному примеру и рассмотрим произвольную пару точек, лежащую внутри круга  – проще всего взять точки . Теперь вычислим криволинейный интеграл двумя способами:

1) По отрезку  прямой . Тут всё элементарно:  и:

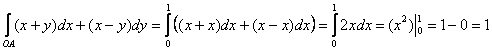
2) По дуге  параболы . В этом случае  и:

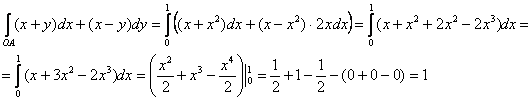
Самостоятельно вычислите этот же интеграл по дуге  кубической параболы . Получится единица.

Или по какой-нибудь простенькой ломаной, например, по ломаной , где . Тоже получится единица!

И вообще – если выбрать любой кусочно-гладкий путь от точки  до точки  (лежащий в области ), то криволинейный интеграл во всех случаях будет равняться единице! Сколь бы длинным и сложным ни был маршрут.

Иными словами, при описанных выше условиях значение криволинейного интеграла не зависит от пути интегрирования.

Но открытия только начинаются!

Если , то подынтегральное выражение является полным дифференциалом некоторой функции двух переменных . Данная функция называется потенциальной или просто потенциалом. Как её найти? Очень просто. Нужно решить  – дифференциальное уравнение в полных дифференциалах.

Для «начинки» нашего нулевого интеграла  таковой функцией является:

И в самом деле, её полный дифференциал:
 – в точности подынтегральное выражение.

Ну и, наверное, все уже поняли, что равенство , которое обеспечивает ноль в формуле Грина, есть не что иное, как равенство смешанных производных 2-го порядка.

Более того, для любых двух точек  и  области  криволинейный интеграл  – равен постоянной величине, которая не зависит от пути интегрирования.

Так, в нашем примере с точками  было совсем не обязательно перебирать множество маршрутов – достаточно найти потенциальную функцию  (решив ДУ в полных дифференциалах) и вычислить криволинейный интеграл по формуле:

Разность  называют разностью потенциалов, и я так вижу, у физиков уже появился здоровый блеск в глазах =) Поэтому не буду томить вас ожиданием и сразу перейду к изложению «главного» физического смысла криволинейного интеграла 2-го рода:

Источник: http://mathprofi.ru/ki_po_zamknutomu_konturu_formula_grina.html

Ориентация границы плоской области.

Напомним, что областью в (boldsymbol{R}^{2}) называется открытое связное множество, а замыкание области получается присоединением к области ее границы.

Теорема Жордана утверждает, что любая простая (без точек самопересечения) замкнутая кривая разделяет плоскость на две области, ограниченную и неограниченную, общей границей которых она является.

Рис. 51.1

Область (Omega subset boldsymbol{R}^{2}) называется односвязной, если для любого простого контура (gamma subset Omega) ограничиваемая этим контуром область (Omega_{1} subset Omega). В частности, область на рис. 51.1 односвязна.

Будем говорить, что простой контур (Gamma) ориентирован положительно, если при обходе контура ограничиваемая им область остается слева (рис. 51.1). Противоположно ориентированный контур будем обозначать через (Gamma^{-}).

Источник: http://univerlib.com/mathematical_analysis/curve_surface_integrals/green_formula_on_plane/

Основные свойства криволинейных интегралов II рода

Приизменении направления интегрирования интеграл меняет свой знак:

Сказанноеверно и для замкнутой кривой, при этом выбор точки начала обхода безразличен.Положительным направлением обхода считается то, при котором область,ограниченная этой кривой, остается слева (для плоской кривой это движение противчасовой стрелки).

Остальные свойства такие же, как и у криволинейного интеграла I рода.

Источник: http://100task.ru/sample/155.aspx

Вычисление криволинейного интеграла II рода

1. Еслипространственная кривая  задана параметрическими уравнениями

причемперемещение от точки  к точке  происходит при изменении параметра  от  до , то

2.  В частном случае для плоской кривой

причемперемещение от точки  к точке  происходит при изменении параметра  от  до . Криволинейный интегралвычисляется по формуле:

3. Еслиплоская кривая  определена уравнением , причем перемещение отточки  к точке  происходит при изменении  от  до , то

Источник: http://100task.ru/sample/155.aspx

Работа векторного поля

Пусть материальная точка под воздействием силы векторного поля  совершает движение в плоскости и проходит путь . Тогда работа векторного поля по перемещению этой точки определяется формулой: . Данная величина стандартно измеряется в Джоулях, но в математических задачах размерность почти никогда не указывается, и я тоже буду придерживаться этого стиля.

Давайте разбираться. Приведу не совсем строгий, но зато вполне понятный пример: представьте, что у вас на столе лежит плоский и достаточно тонкий магнит. Из жизненного опыта все хорошо знают, что чем ближе поднести к нему какую-нибудь железку, тем сильнее она будет притягиваться. В физике это «сильнее» измеряется векторной величиной под названием напряжённость магнитного поля:

– каждой точке  поверхности стола ставится в соответствие несвободный вектор , указывающий направление действия силы (магнитного поля) и её величину в данной точке (чем ближе к магниту, тем длиннее вектор). Множество этих векторов (рассматриваем только плоскость) образует двумерное векторное поле. Такое поле можно формализовать векторной функцией скалярного аргумента:

И в самом деле, если мы начнём подставлять координаты  различных точек (скалярные аргументы), то «на выходе» будем получать различные векторы . Чтобы было понятнее, приведу конкретный пример:  – найдём значение этой функции, например, в точке :

 – в результате получен вектор, который, повторюсь, привязан к точке  и свободному перемещению не подлежит! Догадайтесь с одного раза, почему.

Теперь недалеко от магнита бросим железную пылинку, которая под действием силы магнитного поля проделает путь  (за некоторое время). Таким образом, данное векторное поле совершило работу  по перемещению этой пылинки. А вы как думали? – работают даже магниты! Всегда вспоминайте об этом, когда устанете от какой-нибудь работы =)

И совсем понятный пример находится у многих под рукой, а именно компьютерная мышка – переместите её по произвольной траектории. Сила ваших мускулов совершила работу по перемещению мыши. Следует однако отметить, что обывательское и физическое понимание работы отличаются, и к этому вопросу я вернусь буквально через несколько строк:

Пример 12

Вычислить непосредственно и с помощью формулы Грина работу векторного поля  по контуру, представляющему собой треугольник с вершинами в начале координат и точках ,  (контур интегрирования следует обходить против движения часовой стрелки).

Краткое решение и ответ в конце урока. И не такое оно, между прочим, простое, как может показаться

Не удивляйтесь, если работа будет получаться отрицательной – знаки «плюс» и «минус» указывают направление действия силы. Так, если вы переместите мышь вправо, то, условно говоря, совершите работу . Теперь возвращаем её в исходную точку (не обязательно по той же траектории) и предполагаем, что усилий затрачено столько же. Тот факт, что сила ваших мускулов работала в противоположном направлении, и выражается знаком «минус»: .

Вы поработали? Безусловно. Хотя и не перетрудились =) Но с точки зрения физики работы не совершено! И действительно, работа по замкнутому контуру составила . Вот так вот своими руками вы смоделировали особый вид поля!

Если интеграл по замкнутому контуру равен нулю, то соответствующее векторное поле называют потенциальным. Проверим, будет ли оно таковым в Примере 12:

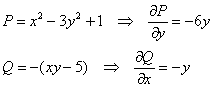
, следовательно, потенциальной функции не существует и поле  не потенциально. Поэтому можно сразу сказать, что

Кстати, такое задание иногда встречается: проверить будет ли данное поле потенциальным и если да, то найти его потенциал. Напоминаю, что для нахождения потенциальной функции нужно решить дифференциальное уравнение в полных дифференциалах. Что делать в пространственном случае – смотрите в статье о теории поля.

И в заключение урока мы как раз немного поговорим

о криволинейных интегралах в пространстве

А почему нет? Никто же не запрещает интегрировать по пространственным кривым. Наоборот – все только разрешают =)

На самом деле я мог бы начать и с них, но, во-первых, такие задачи значительно реже встречаются на практике, и, во-вторых, возникла бы неслабая путаница.

Пространственная кривая, как правило, задаётся параметрическими уравнениями , и по большому счёту новизна состоит в дополнительной координате.

Так, например, криволинейный интеграл 1-го рода, рассчитывается по формуле:
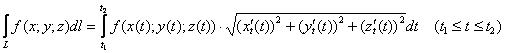, и его физический смысл – это масса пространственной кривой , где  – функция её плотности.

Криволинейный интеграл 2-го рода запишется в виде:
, и, наверное, вы уже догадываетесь, как его решать. Осталось подтвердить свою догадку решением заключительного примера:

Пример 13

Вычислить криволинейный интеграл , где  – первый виток винтовой линии .

Тот, кто хорошо разобрался с параметрическими уравнениями окружности, легко представит эту линию в уме. Впрочем, информацию не сложнее разыскать в Сети.

Аналогично – предложенный криволинейный интеграл можно интерпретировать, как работу трёхмерного векторного поля  по перемещению материальной частицы вдоль пространственной кривой .

Не так давно я оговорился, что работа – есть «главный» физический смысл криволинейного интеграла. Здесь я имел в виду, что задача на работу силы – самая известная. Криволинейные интегралы находят широчайшее применение в физике, и с помощью них можно подсчитать много других величин.

И, к слову, термин «поле» – он не физический, а относится именно к математике. Силовые же физические поля – лишь частные примеры. Обязательно ознакомьтесь с увлекательной теорией поля!

Но это после того, как будет покончено с интегралами. Ещё существуют поверхностные. Впрочем, уж они-то после всех испытаний – так, ерунда =)

Желаю успехов!

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

«Всё сдал!» — онлайн-сервис помощи студентам

Источник: http://mathprofi.ru/ki_po_zamknutomu_konturu_formula_grina.html

Формула Грина

Интеграл по замкнутому контуру  можнопреобразовать в двойной интеграл по области , ограниченной этим контуром, и наоборот, используяформулу Грина:

где функции  и  и их частные производные первого порядкадолжны быть непрерывными в области  и на контуре .

При этом обход контура  выбирается таким образом, что область  остается слева.

Источник: http://100task.ru/sample/155.aspx

Условие независимости криволинейного интеграла от пути интегрирования

Для того, чтобыкриволинейный интеграл

не зависел от путиинтегрирования, необходимо и достаточно, чтобы выполнялось равенство

Если же, крометого,  есть замкнутая кривая, то

Источник: http://100task.ru/sample/155.aspx

Примеры решения задач

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.

Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.

Источник: http://100task.ru/sample/155.aspx