Всё просто: биссектриса угла — это луч с началом в вершине угла, который делит этот угол пополам
Длина биссектрисы треугольника
Рассмотрим треугольник на Рис.5.
Длина биссектрисы треугольника можно вычислить следующими формулами:
где p − полупериметр треугольника ABC, ( small gamma -) угол между биссектрисой ( small l_c) и вершиной ( small h_c:)
Доказательство. 1) Из теоремы Стюарта следует:
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
Поскольку 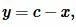 то (2) можно переписать так:
то (2) можно переписать так:
Найдем x из (3):
Тогда:
или
Подставим (4) и (5) в (1):
или
Cледовательно
Доказательство. 2) Подставим (4) и (5) в (6):
Тогда
Доказательство. 3) Сделаем следующее обозначение:
Сделаем преобразования формулы (7), учитывая (9):
Следовательно
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
Учитывая, что 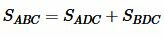 , получим:
, получим:
или
Тогда
Для ( small sin C ) применим формулу синуса двойного угла:
Подставляя (12) в (11) получим:
то есть
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
Тогда
Остается показать, что 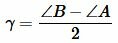 .
.
Поскольку биссектриса lc делит угол C пополам, то:
Далее
Тогда
Подставляя (14) в (15), получим:
или
Источник: http://matworld.ru/geometry/bissektrisa-treugolnika.php
Основное свойство биссектрисы угла
На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:
Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.
В переводе с математического на русский это означает сразу два факта:
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:
Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.
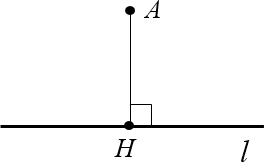 Графическое представление расстояния от точки до прямой
Графическое представление расстояния от точки до прямой
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:
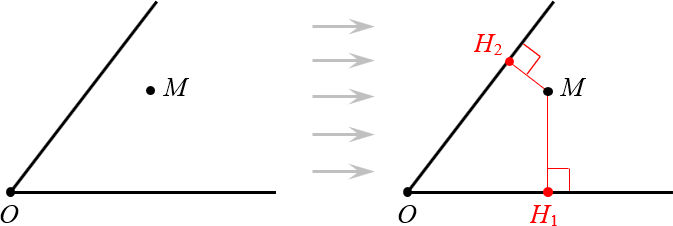 Определяем расстояние от точки до сторон угла
Определяем расстояние от точки до сторон угла
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.
Как и обещал, разобьём доказательство на две части:
1. Расстояния от точки на биссектрисе до сторон угла одинаковы
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:
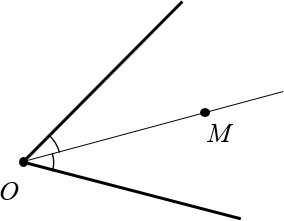
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:
Провели перпендикуляры к сторонам угла
Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:
- $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
- $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
- $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)
2. Если расстояния равны, то точка лежит на биссектрисе
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:
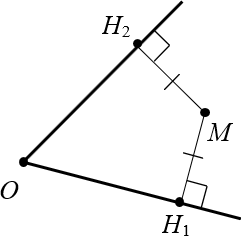
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.
Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:
Провели луч $OM$ внутри угла
Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:
- Гипотенуза $OM$ — общая;
- Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
- Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.
Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.
В заключение доказательства отметим красными дугами образовавшиеся равные углы:
Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных
Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)
Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.
Смотрите также:
- Высота в треугольнике

- Основное свойство биссектрисы угла в треугольнике и его применение для решения задач

- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)

- Правила вычисления производных

- Сводный тест по задачам B15 (2 вариант)

- Симметрия корней и оптимизация ответов в тригонометрии

Источник: http://berdov.com/docs/treugolnik/bissektrisa-ugla/