Двоичное кодирование информации

Онлайн перевод текста в двоичный код — профессиональная кодировка текста в двоичного кода. Загрузите файл или впишите свой текст, а наш инструмент переведет его в код.

Кодировка текста в двоичного код

Введите или вставьте свой двоичный файл:

Как использовать двоичный конвертер?

Это действительно просто!

1. Введите или вставьте текст в первое поле.
2. Нажмите кнопку «Преобразовать», чтобы преобразовать текст в двоичный код.
3. Выходные данные двоичного кода будут отображаться во втором поле автоматически по мере ввода.
4. При желании вы можете скопировать вывод в буфер обмена или сохранить его как файл на своем устройстве.

Связанные инструменты:

• Перевод двоичного кода в текст

• Генератор QR-кода

• Генератор Robots.txt

• Генератор Sitemap XML

• Кодировщик / декодер URL или текста

• Генератор Md5 онлайн

• Преобразовать картинку в base64

• Преобразовать base64 в картинку

• Сравнить 2 текста, кода

С английского на двоичный

Существуют ASCII и двоичные представления для множества символов; пробелы, знаки препинания и буквы. А пока мы сосредоточимся на том, как переводить двоичный текст, используя только буквы. Первое, что нам нужно, это слово. Давайте использовать «собака», потому что кто не любит собак?

Мы должны разбить слово на каждую букву; dog и обратитесь к нашей таблице ASCII. В ASCII каждому символу назначается десятичная дробь . Важно помнить, что двоичные и десятичные числа в верхнем и нижнем регистрах не идентичны. В противном случае компьютер, читающий двоичный код, не будет знать, какие буквы нужно использовать с заглавной буквы. Давайте посмотрим на таблицу ASCII. Обратите внимание, что это только часть таблицы. Вы можете найти обширный набор ASCII для двоичных таблиц в интернете; на этом сайте вы найдете таблицы преобразования алфавита ASCII в двоичную кодировку как для строчных, так и для прописных букв.

Мы видим, что символы dog соответствуют десятичным дробям 100, 111 и 103. Единственное, что осталось сделать, чтобы преобразовать наш текст в двоичный код, — это преобразовать десятичные числа в двоичный. Начиная со 100, нам нужно переопределить число, используя степень двойки.

Поскольку 100 не является степенью 2, найдите степень 2, которая равна или меньше 100. Мы можем переопределить 100 как 64 + 36. Поскольку 36 не является степенью 2, нам нужно переопределить это тоже. К счастью для нас, 36 можно переопределить как 32 + 4; больше степеней 2.

Начиная с 2 0 , давайте посчитаем, какие степени двойки мы использовали, и обозначим их единицей. Неиспользуемые степени двойки обозначаются нулем.

В двоичном формате буква всегда представлена ​​одним байтом из восьми битов или цифрами. Но наш двоичный вывод состоит всего из семи цифр. Как это исправить? Довольно просто — в начале нитки прихватываем ноль . Когда вы используете преобразователь текста в двоичный, этот шаг выполняется автоматически.

Почему ноль? Мы не можем использовать единицу без изменения всего значения двоичного кода. А в двоичном формате текстовые символы всегда начинаются с 010 или 011.  010 обозначает заглавную букву, а 011 обозначает строчную. Мы знаем, что наши буквы строчные, и если мы добавим этот ноль, у нас будет префикс 011. Теперь, когда мы добавили ноль, давайте посмотрим, что такое наш двоичный код. В двоичном формате «собака» выглядит так: 01100100 01101111 01100111.

Если вы хотите вставить в текст пробел, для этого тоже есть двоичный код. Простое нажатие клавиши пробела между символами на самом деле не означает пробел. Если мы хотим добавить второе слово к нашей фразе, нам понадобится двоичная строка « 00100000 » для разделения слов.

Представьте, что мы хотим сказать «хорошая собака». Во-первых, нам нужно найти десятичное значение первого слова. В кодировке ASCII «хорошо» представлены числами 103, 111, 111 и 100. Это те же десятичные дроби в первом слове, dog, так что вы уже знаете их двоичный вывод. Просто переставьте их, и вы сможете записать «хорошо» в двоичном формате.

Теперь давайте сложим их все вместе и не забываем строку, которая нам нужна для пробела между двумя словами. Вы можете использовать переводчик текста в двоичный код на этой странице, чтобы увидеть, как он должен выглядеть. Как вы, наверное, догадались, для короткой фразы это много двоичного кода. Переводчик с английского на двоичный полезен, если вам нужно преобразовать большой текст.

Что такое «привет» в двоичном коде?

Слово «привет» в двоичном коде выглядит следующим образом: 0110100001100101011011000110110001101111. Разделив его на восьмизначные сегменты, легче увидеть двоичный байт, соответствующий каждой букве: 01101000 01100101 01101100 01101100 01101111

Таблица двоичного преобразования

Символ ASCII	Шестнадцатеричные	Двоичные
NUL	00	00000000
SOH	01	00000001
STX	02	00000010
ETX	03	00000011
EOT	04	00000100
ENQ	05	00000101
ACK	06	00000110
BEL	07	00000111
BS	08	00001000
HT	09	00001001
LF	0A	00001010
VT	0B	00001011
FF	0C	00001100
CR	0D	00001101
SO	0E	00001110
SI	0F	00001111
DLE	10	00010000
DC1	11	00010001
DC2	12	00010010
DC3	13	00010011
DC4	14	00010100
NAK	15	00010101
SYN	16	00010110
ETB	17	00010111
CAN	18	00011000
EM	19	00011001
SUB	1A	00011010
ESC	1B	00011011
FS	1C	00011100
GS	1D	00011101
RS	1E	00011110
US	1F	00011111
Space	20	00100000
!	21	00100001
«	22	00100010
#	23	00100011
$	24	00100100
%	25	00100101
&	26	00100110
‘	27	00100111
(	28	00101000
)	29	00101001
*	2A	00101010
+	2B	00101011
,	2C	00101100
—	2D	00101101
.	2E	00101110
/	2F	00101111
0	30	00110000
1	31	00110001
2	32	00110010
3	33	00110011
4	34	00110100
5	35	00110101
6	36	00110110
7	37	00110111
8	38	00111000
9	39	00111001
:	3A	00111010
;	3B	00111011
<	3C	00111100
=	3D	00111101
>	3E	00111110
?	3F	00111111
@	40	01000000
A	41	01000001
B	42	01000010
C	43	01000011
D	44	01000100
E	45	01000101
F	46	01000110
G	47	01000111
H	48	01001000
I	49	01001001
J	4A	01001010
K	4B	01001011
L	4C	01001100
M	4D	01001101
N	4E	01001110
O	4F	01001111
P	50	01010000
Q	51	01010001
R	52	01010010
S	53	01010011
T	54	01010100
U	55	01010101
V	56	01010110
W	57	01010111
X	58	01011000
Y	59	01011001
Z	5A	01011010
[	5B	01011011
	5C	01011100
]	5D	01011101
^	5E	01011110
_	5F	01011111
`	60	01100000
a	61	01100001
b	62	01100010
c	63	01100011
d	64	01100100
e	65	01100101
f	66	01100110
g	67	01100111
h	68	01101000
i	69	01101001
j	6A	01101010
k	6B	01101011
l	6C	01101100
m	6D	01101101
n	6E	01101110
o	6F	01101111
p	70	01110000
q	71	01110001
r	72	01110010
s	73	01110011
t	74	01110100
u	75	01110101
v	76	01110110
w	77	01110111
x	78	01111000
y	79	01111001
z	7A	01111010
{	7B	01111011
|	7C	01111100
}	7D	01111101
~	7E	01111110
DEL	7F	01111111

Источник: http://sas.com.ru/text-to-binary

Двоичный текст

Converts from Binary to Text

Бинарная система чисел, или система чисел base-2, представляет числовые значения с использованием двух символов, 0 и 1. Более конкретно, обычная система base-2 представляет собой позиционную нотацию с радиусом 2. Благодаря своей простой реализации в цифровых электронных схемах с использованием логических ворот, бинарная система используется внутри всех современных компьютеров.

Source: Wikipedia

AKA:

Источник: http://online-toolz.com/langs/ru/tool-ru-text-binary-convertor.html

Почему в компьютере используется двоичный код

Люди для записи текстовой информации используют буквы. В русском языке их 33. Комбинациями из десяти цифр (от 0 до 9) мы записываем числовые данные. При работе с графической информацией пользуемся палитрой из миллионов цветов. Наши уши различают звуки в диапазоне от 16 до 20000 Гц.

Если добавить к этому обоняние, вкусовые и тактильные ощущения, получится огромнейшее разнообразие информационных импульсов, которые может воспринимать, хранить и обрабатывать наш мозг.

При помощи технических средств невозможно воссоздать аналогичную систему работы с информацией.

Людям проще всего создавать приборы, принимающие одно из двух состояний: лампочка горит или нет, магнитное поле есть или его нет и т.д. И значительно сложнее, например, заставить лампочку в разных ситуациях светиться одним из 10 цветов. Не говоря уже о 10 миллионах цветов, воспринимаемых человеком.

В технике намного удобнее иметь дело с множеством простых элементов, чем с небольшим количеством сложных.

Чтобы иметь возможность хранить и обрабатывать информацию техническими средствами, люди решили переводить ее на максимально простой «язык», состоящий всего из двух «букв» – так называемый

двоичный

или

бинарный

код.

Используя разные комбинации большого количества двух символов, в бинарном коде можно зашифровать любую числовую, текстовую, звуковую или графическую информацию.

Компьютер же является ничем иным, как машиной, предназначенной для хранения и обработки информации в таком виде.

Перевод данных в двоичный код называется

кодированием

.

Противоположный процесс, в результате которого бинарный код превращается в привычную для людей информацию, называется

декодированием

.

Компьютер осуществляет кодирование «на лету» при получении данных извне: ввод текста пользователем с клавиатуры, запись видео с веб-камеры, запись звука с микрофона и т.д.

Перед выводом информации на экран, в аудиосистему или же ее распечатыванием, происходит обратный процесс (декодирование).

Как осуществляется кодирование различных типов данных, рассмотрим немного ниже. Сначала давайте разберемся, из каких же символов формируется двоичный код внутри компьютера и как он там хранится.

С технической стороны компьютерный двоичный код реализуется наличием или отсутствием определенных свойств (импульсов) у мельчайших запоминающих элементов. Эти импульсы могут быть:

• фотооптическими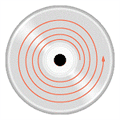

Так, поверхность любого

оптического диска

(CD, DVD или BluRay) состоит из спирали, которую формируют мелкие отрезки. Каждый из них может быть либо темного, либо светлого цвета. Диск быстро вращается в дисководе. На его спиральной дорожке фокусируется лазер, отражение которого попадает на фотоэлемент. Темные участки спирали поглощают свет и не передают его на фотоэлемент, светлые – наоборот, отражая свет, передают импульс фотоэлементу. В результате фотоэлемент получает информацию, зашифрованную в дорожке диска в виде темных и светлых точек.

• магнитными

Например, внутри

жесткого диска

находится быстро вращающаяся пластина. Вся ее поверхность тоже представляет собой спираль, состоящую из последовательности миллионов мелких участков. Каждый из них является элементом, который может принимать одно из двух состояний: «намагниченное», «ненамагниченное». Эти элементы и формируют двоичный код, в котором кодируется какая-то информация. Считывание состояния элементов осуществляется специальной головкой, которая быстро движется по поверхности пластины;

• электрическими

Например,

оперативная память

компьютера является микросхемой, состоящей из миллионов маленьких ячеек, созданных из микроскопических транзисторов и конденсаторов. Каждая такая ячейка может либо содержать электрический заряд, либо нет. Комбинации заряженных и разряженных ячеек оперативной памяти и формируют в ней двоичный код.

В аналогичной форме информация хранится и во всех других запоминающих микросхемах (флешки, SSD-носители и др.).

Процессор

компьютера обрабатывает двоичный код тоже в виде электрических импульсов.

Иногда можно встретить ошибочное мнение, что бинарный код внутри компьютера записан в виде обычных нулей и единиц. Это следствие непонимания технической стороны вопроса. Привычных для нас

нулей и единиц в компьютере нет

. «Символами» компьютерного двоичного кода является наличие или отсутствие у мельчайшего запоминающего элемента определенного свойства (см. выше).

Чтобы было нагляднее, в учебных материалах отсутствие у элемента такого свойства

лишь условно

обозначают нулем, а его наличие – единицей. Но с таким же успехом их можно бы было обозначать точкой и тире или крестиком и ноликом.

Источник: http://chaynikam.info/dvoichnoe-kodirovanie.html

Отличный план

Чтобы объяснить всё это, нам понадобится несколько тезисов:

1. Система записи числа — это шифр.
2. Мы привыкли шифровать десятью знаками.
3. Но система записи чисел может быть любой. Это условность.
4. Двоичная система — это тоже нормальная система.
5. Всё тлен и суета.

Источник: http://zen.yandex.ru/media/code/dvoichnoe-schislenie-na-palcah-5e26d5cd32335400ac8daaef

Система записи — это шифр

Если у нас есть девять коров, мы можем записать их как или как 9 × .

Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.

Допустим, к нашему стаду прибиваются ещё . Теперь у нас — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.

Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × — это не то же самое, что . Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.

Источник: http://zen.yandex.ru/media/code/dvoichnoe-schislenie-na-palcah-5e26d5cd32335400ac8daaef

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

110100001001101011010000101111101101000010110100

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

15-6-2-16-13-30-26-16-11 17-18-10-14-6-18

Шифрование публичным ключом

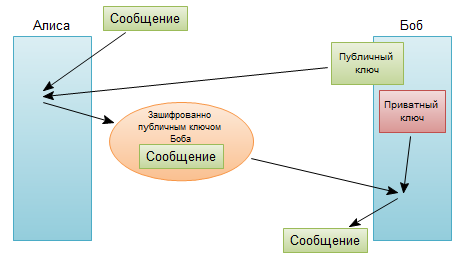
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139

Источник: http://tproger.ru/translations/10-codes-and-ciphers/

Кодирование числовой информации

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: 0 1 2 3 4 5 6 7 8 9. Эта система называется

десятичной

.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до 9), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до 99, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до 999 и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры — логический ноль (отсутствие у бита какого-то свойства) и логическая единица (наличие у бита этого свойства).

Система счисления, использующая только две цифры, называется

двоичной

.

При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

Вот таблица первых десяти чисел в каждой из этих систем счисления:

Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно 1 разряда. В двоичной системе для тех же целей потребуется уже 4 разряда.

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум 4 бита (0,5 байта).

Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус — необходимость иметь дело с большим количеством разрядов.

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы — 255, в 16 разрядах – 65535, в 24 разрядах – 16777215.

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

• небольшие целые числа без знака

Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется 1 байт (8 битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

• большие целые числа и числа со знаком

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится 2-байтний блок (16 битов).

Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком «плюс», этот бит остается пустым, если со знаком «минус» – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах.

Например, алгоритм кодирования числа +2676 будет следующим:

1. Перевести число 2676 из десятичной системы счисления в двоичную. В итоге получится 101001110100;

2. Записать полученное двоичное число в первые 15 бит 16-битного блока (начиная с правого края). Последний, 16-й бит, должен остаться пустым, поскольку кодируемое число имеет знак +.

В итоге +2676 в двоичном коде на запоминающем устройстве будет выглядеть так:

Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

Чтобы было понятно, рассмотрим алгоритм кодирования числа -2676:

1. Перевести число 2676 из десятичной системы счисления в двоичную. Получим все тоже двоичное число 101001110100;

2. Записать полученное двоичное число в первые 15 бит 16-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из 15 битов;

3. Записать в 16-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

В итоге -2676 на запоминающем устройстве в двоичном коде будет иметь следующий вид:

Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в 15 битах запоминающего устройства, является 32767.Иногда для записи чисел по этому алгоритму выделяются 4-байтные блоки. В таком случае для кодирования каждого числа будет использоваться 31 бит плюс 1 бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет 2147483647 (со знаком плюс или минус).

• дробные числа со знаком

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых

чисел с плавающей запятой

(точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет 4-байтную ячейку (32 бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком «плюс» – бит остается пустым.

• во втором слева бите аналогичным образом записывается знак

порядка

(что такое порядок поймете позже);

• в следующих за ним 7 битах записывается значение порядка.

• в оставшихся 23 битах записывается так называемая

мантисса

числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число 6,25.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное 6,25 равно двоичному 110,01);

2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу ,11001;

3. Определить значение и знак порядка.

Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно 3 (или 11 в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс»;

Таким образом, порядок двоичного числа 110,01 будет равен +11, а его мантисса ,11001. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается.

Числа с плавающей запятой, кодируемые в 32 битах, называю

числами одинарной точности

.

Когда для записи числа 32-битной ячейки недостаточно, компьютер может использовать ячейку из 64 битов. Число с плавающей запятой, закодированное в такой ячейке, называется

числом двойной точности

.

Источник: http://chaynikam.info/dvoichnoe-kodirovanie.html

Мы привыкли шифровать десятью знаками

У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.

Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.

Например, перед нами число 19 547. Мы знаем, что в нём есть:

1 × 10 000

9 × 1000

5 × 100

4 × 10

7 × 1

Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:

1 × 10⁴

9 × 10³

5 × 10²

4 × 10¹

7 × 10⁰

Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.

Источник: http://zen.yandex.ru/media/code/dvoichnoe-schislenie-na-palcah-5e26d5cd32335400ac8daaef

Онлайн сервисы для расшифровки

Если все же требуется увидеть расшифрованный бинарный код, раскодировать слова, либо, наоборот, перевести их в двоичную форму, проще всего использовать онлайн-сервисы, предназначенные для этих целей.

Два окна, привычных для онлайн-переводов позволяют практически одновременно увидеть оба варианта документа в обычной и бинарной форме.  Расшифровка осуществляется в обе стороны.  Ввод текста на русском или английском языках производится простым копированием и вставкой.

Источник: http://godnyesovety.ru/1052-rasshifrovka-binarnogo-koda-onlayn-instrumenty-gde-primenyaetsya.html

Кодирование изображений в двоичный код

Чтобы сохранить в двоичном коде фотографию, ее сначала виртуально разделяю на множество мелких цветных точек, называемых

пикселями

(что-то на подобии мозаики).

После разбивки на точки цвет каждого пикселя кодируется в бинарный код и записывается на запоминающем устройстве.

Если говорят, что размер изображения составляет, например, 512 х 512 точек, это значит, что оно представляет собой матрицу, сформированную из 262144 пикселей (количество пикселей по вертикали, умноженное на количество пикселей по горизонтали).

Прибором, «разбивающим» изображения на пиксели, является любая современная фотокамера (в том числе веб-камера, камера телефона) или сканер.

И если в характеристиках камеры значится, например, «10 Mega Pixels», значит количество пикселей, на которые эта камера разбивает изображение для записи в двоичном коде, — 10 миллионов.

Чем на большее количество пикселей разделено изображение, тем реалистичнее выглядит фотография в декодированном виде (на мониторе или после распечатывания).

Однако качество кодирования фотографий в бинарный код зависит не только от количества пикселей, но также и от их цветового разнообразия.

Алгоритмов записи цвета в двоичном коде существует несколько. Самым распространенным из них является

RGB

. Эта аббревиатура – первые буквы названий трех основных цветов: красного – англ.

R

ed, зеленого – англ.

G

reen, синего – англ.

B

lue.

Из школьных уроков рисования, Вам, наверное, известно, что смешивая эти три цвета в разных пропорциях, можно получить любой другой цвет или оттенок.

На этом и построен алгоритм RGB. Каждый пиксель записывается в двоичном коде путем указания количества красного, зеленого и синего цвета, участвующего в его формировании.

Чем больше битов выделяется для кодирования пикселя, тем больше вариантов смешивания этих трех каналов можно использовать и тем значительнее будет цветовая насыщенность изображения.

Цветовое разнообразие пикселей, из которых состоит изображение, называется

глубиной цвета

.

Если для кодирования каждого пикселя какого-то изображения выделяется 8 битов двоичного кода, цветовое разнообразие составит 256 цветов.

Глубина цвета 12-битов даст 4096 цветов, 16-битов — 65536 цветов, 18-битов — 262144 цветов.

Максимальная глубина цвета, используемая в компьютерной технике — 24 бита. Такую глубину часто называют

True Color

(«Настоящий цвет»). Она позволяет отобразить около 16,7 млн. цветов. Глаз человека не способен воспринимать большее их количество.

Тем не менее, часто встречается и так называемая 32-битная глубина цвета. Она не предусматривает увеличение количества оттенков. Дополнительные биты, выделяемые для кодирования каждого пикселя, предназначены для регулирования степени его прозрачности или же не используются.

Описанная выше техника формирования изображений из мелких точек является наиболее распространенной и называется

растровой

. Но кроме растровой графики, в компьютерах используется еще и так называемая

векторная

графика.

Векторные изображения создаются только при помощи компьютера (фотокамеры этого делать «не умеют») и формируются не из пикселей, а из графических примитивов (линий, многоугольников, окружностей и др.).

Зачем нужна векторная графика? В известной детской песенке поется, что для изображения «человечка» достаточно нарисовать всего две «палки» и «огуречек». А представьте, насколько трудно вручную составить человечка из большого числа точек.

Векторная графика — это

чертежная графика

. Она очень удобна для компьютерного «рисования» и широко используются дизайнерами при графическом оформлении печатной продукции, в том числе создании огромных рекламных плакатов, а также в других подобных ситуациях.

Векторное изображение в двоичном коде записывается как совокупность примитивов с указанием их размеров, цвета заливки, места расположения на холсте и некоторых других свойств.

Например, чтобы записать на запоминающем устройстве векторное изображение круга, компьютеру достаточно в двоичный код закодировать тип объекта (окружность), координаты его центра на холсте, длину радиуса, толщину и цвет линии, цвет заливки.

В растровой системе пришлось бы кодировать цвет каждого пикселя. И если размер изображения большой, для его хранения понадобилось бы значительно больше места на запоминающем устройстве.

Тем не менее, векторный способ кодирования не позволяет записывать в двоичном коде реалистичные фото. Поэтому все фотокамеры работают только по принципу растровой графики. Рядовому пользователю иметь дело с векторной графикой в повседневной жизни приходится не часто.

Источник: http://chaynikam.info/dvoichnoe-kodirovanie.html

Кодирование звуковой информации

Любой звук, слышимый человеком, является колебанием воздуха, которое характеризируется двумя основными показателями: частотой и амплитудой.

Амплитуда колебаний — это степень отклонения состояния воздуха от начального при каждом колебании. Она воспринимается нами как громкость звука.

Частота колебаний — это количество отклонений состояний воздуха от начального за единицу времени. Она воспринимается как высота звука.

Так, тихий комариный писк — это звук с высокой частотой, но с небольшой амплитудой. Звук грозы наоборот имеет большую амплитуду, но низкую частоту.

Если графически изобразить звуковую волну, она будет выглядеть следующим образом:

Схему работы компьютера со звуком в общих чертах можно описать так.

Микрофон превращает колебания воздуха в аналогичные по характеристикам электрические колебания.

Звуковая карта компьютера «умеет» преобразовывать электрические колебания в двоичный код, который записывается на запоминающем устройстве. При воспроизведении такой записи происходит обратный процесс (декодирование) — двоичный код преобразуется в электрические колебания, которые поступают в аудиосистему или наушники.

Динамики акустической системы или наушников имеют противоположное микрофону действие. Они превращают электрические колебания в колебания воздуха.

Но каким же образом звуковая карта преобразовывает электрические колебания в двоичный код?

Если взглянуть на графическое изображение волны и внимательно проанализировать ее геометрию, можно увидеть, что в каждый конкретный момент времени звук имеет определенную интенсивность (степень отклонения от начального состояния).

Значит если весь отрезок времени, в течение которого длится звук, разделить на очень маленькие временные участки, то звуковую волну можно будет записать как очередность значений интенсивности звука в каждом таком временном участке.

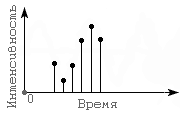
Но частота «дробления» звука должна быть достаточно высокой, иначе значения участков не будут отображать реальную геометрию волны. Вот примеры слишком низкой частоты дробления.

Описанный принцип разделения звуковой волны на мелкие участки и лежит в основе двоичного кодирования звука.

Аудиокарта компьютера разделяет звук на очень мелкие временные участки и кодирует степень интенсивности каждого из них в двоичный код. Такое «дробление» звука на части называется

дискретизацией

. Чем выше частота дискретизации, тем точнее фиксируется геометрия звуковой волны и тем качественней получается запись.

Так, простая речь (например, диктофонная запись) нормально воспринимается человеком, если частота дискретизации при кодировании была не ниже 8000 Гц (8 КГц). То есть, каждая секунда такой записи в двоичном коде должна состоять как минимум из 8000 частей.

Музыкальные же произведения, хранимые в компьютере, должны иметь еще более высокую частоту дискретизации. При записи стандартных звуковых CD она составляет минимум 44,1 КГц (44100 Гц).

Качество записи сильно зависит также от количества битов, используемых компьютером для кодирования каждого участка звука, полученного в результате дискретизации.

Представим, например, что для кодирования каждого такого участка компьютер использует 8 битов. Как известно, 8-битная ячейка может принимать одно из 256 значений. Но вдруг разнообразие интенсивности участков, полученных при дискретизации какого-то звука, оказалось более широким (например, 512 вариантов). В таком случае, компьютер «округлит» интенсивность участков до ближайших доступных значений чтобы «уложиться» в 256 вариантов и качество записи получится низким.

Количество битов, используемых для кодирования каждого участка звука, полученного при дискретизации, называется

глубиной звука

.

Глубины звука в 8-битов достаточно для кодирования простой речи. Но музыкальные произведения с такой глубиной будут звучать отвратительно. Поэтому гораздо чаще встречаются звуковые файлы, закодированные с глубиной 16, 24 или даже 32 бита.

Следует учитывать, что далеко не все устройства, предназначенные для воспроизведения «цифрового» звука, могут работать с файлами, закодированными с высокой частотой дискретизации и/или большой глубиной звука. Такие файлы могут проигрываться на одном компьютере, и «не открываться» на другом (если звуковая карта не поддерживает настолько высокий уровень дискретизации или глубины звука).

Источник: http://chaynikam.info/dvoichnoe-kodirovanie.html

Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)

Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.

Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить ?⚫⚫ и ⚫⚫?, получится ?⚫?. Мы писали об этом подробнее в статье о сложении через транзисторы.

Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.

И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.

При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.

Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.

Источник: http://zen.yandex.ru/media/code/dvoichnoe-schislenie-na-palcah-5e26d5cd32335400ac8daaef

Особенности бинарного кодирования видео

Видеозапись состоит из двух компонентов: звукового и графического.

Кодирование звуковой дорожки видеофайла в двоичный код осуществляется по тем же алгоритмам, что и кодирование обычных звуковых данных (см. предыдущий пункт).

Принципы кодирования видеоизображения схожи с кодированием растровой графики (рассмотрено выше), хотя и имеют некоторые особенности.

Как известно, видеозапись — это последовательность быстро меняющихся статических изображений (кадров). Одна секунда видео может состоять из 25 и больше картинок. При этом, каждый следующий кадр лишь незначительно отличается от предыдущего.

Учитывая эту особенность, алгоритмы кодирования видео, как правило, предусматривают запись лишь первого (базового) кадра. Каждый же последующий кадр формируются путем записи его отличий от предыдущего.

Источник: http://chaynikam.info/dvoichnoe-kodirovanie.html