Методика и подробные примеры решений, которые позволят справиться практически с любым заданием. Задача с треугольником плоскости
Глава 2. Декартовы прямоугольные координаты на плоскости
Р”
екартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.
Точка пересечения осей называется началом координат, Р° сами РѕСЃРё — координатными РѕСЃСЏРјРё. Первая РёР· координатных осей называется РѕСЃСЊСЋ абсцисс, вторая — РѕСЃСЊСЋ ординат.
Начало координат обозначается Р±СѓРєРІРѕР№ Рћ, РѕСЃСЊ абсцисс — символом РћС…, РѕСЃСЊ ординат — символом РћСѓ.
Координатами произвольной точки М в заданной системе называют числа
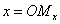 ,
, 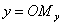
( СЃРј. СЂРёСЃ. 1), РіРґРµ 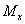 Рё
и 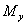 суть проекции точки М на оси Ох и Оу,
суть проекции точки М на оси Ох и Оу,
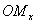 обозначает величину отрезка
обозначает величину отрезка 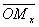 оси абсцисс,
РѕСЃРё абсцисс, 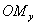 — величину отрезка
— величину отрезка 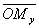 РѕСЃРё ординат. Число С… называется абсциссой точки Рњ, число Сѓ — ординатой этой же точки. РЎРёРјРІРѕР» Рњ(С…; Сѓ) обозначает, что точка Рњ имеет абсциссой число С…, Р° ординатой число Сѓ.
РѕСЃРё ординат. Число С… называется абсциссой точки Рњ, число Сѓ — ординатой этой же точки. РЎРёРјРІРѕР» Рњ(С…; Сѓ) обозначает, что точка Рњ имеет абсциссой число С…, Р° ординатой число Сѓ.
РћСЃСЊ РћСѓ разделяет РІСЃСЋ плоскость РЅР° РґРІРµ полуплоскости; та РёР· РЅРёС…, которая расположена РІ положительном направлении РѕСЃРё РћС…, называется правой, другая — левой. Точно так же РѕСЃСЊ РћСѓ разделяет плоскость РЅР° РґРІРµ полуплоскости; та РёР· РЅРёС…, которая расположена РІ положительном направлении РѕСЃРё РћСѓ, называется верхней, другая нижней.
РћР±Рµ координатные РѕСЃРё вместе разделяют плоскость РЅР° четыре четверти, которые нумеруют РїРѕ следующему правилу: первой координатной четвертью называется та, которая лежит одновременно РІ правой Рё РІ верхней полуплоскости, второй — лежащая РІ левой Рё РІ верхней полуплоскости, третьей — лежащая РІ левой Рё РІ нижней полуплоскости, четвертой — лежащая РІ правой Рё РІ нижней полуплоскости.
| 17 |
Построить точки А(2; 3), В(-5; 1), С(-2; -3), D(0, 3); E(-5; 0), F(-1/3; 2/3). 18 Найти координаты проекций на ось абсцисс точек А (2; 3), B(3; -1), C(-5; 1), D(-3; 2), E(-5; -1). 19 Найти координаты проекция на ось ординат точек А(-3; 2), B(-5; 1), C(3; -2), D(-1; 1), E(-6; -2). 20 Найти координаты точек, симметричных отосительно оси Ох точкам: 20.1 А(2; 3); 20.2 B(-3; 2); 20.3 C(-1; -1); 20.4 D(-3; -5); 20.5 E(-4; -6); 20.6 F(a, b); 21 Найти координаты точек, симметричных относитель оси Оу точкам: 21.1 A(-1; 2); 21.2 B(3; -1); 21.3 C(-2; -2); 21.4 D(-2; 5); 21.5 E(3; -5); 21.6 F(a; b); 22 Найти координаты точек симметричных относительно начала координат точкам: 22.1 A(3; 3); 22.2 B(2; -4); 22.3 C(-2; 1); 22.4 D(5; -3); 22.5 E(-5; -4); 22.6 F(a; b); 23 Найти координаты точек, симметричных относительно начала координат точкам: 23.1 A(2; 3); 23.2 B(5; -2); 23.3 C(C(-3; 4); 24 Найти координаты точек, симметричных относительно биссектрисы второго координатного угла точкам: 24.1 A(3; 5); 24.2 B(-4; 3); 24.3 C(7; -2); 25 Определить, в каких четвертях может быть расположена точка М(x; y), если: 25.1 xy>0; 25.2 xy<0; 25.3 x-y=0; 25.4 x+y=0; 25.5 x+y>0; 25.6 x+y<0; 25.7 x-y>0; 25.8 x-y<0;

Источник: http://a-geometry.narod.ru/problems/problems_02.htm
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
- На плоскости, где достаточно двух координат для описания любых геометрических объектов.
- В трехмерном пространстве, где любая точка имеет три координаты.
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

- Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
- Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
- Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
- Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.
Источник: http://nauka.club/matematika/geometriya/uravnenie-bissektrisy-v-treugolnike.html
Биссектриса — первое
В первом из них имеем у х и графиком функции является биссектриса первого и третьего координатных углов. Во втором случае получаем у — — х, график — биссектриса второго и четвертого координатных углов. [16]
Таким образом, в окрестности угла прямоугольной пластинки, свободно опертой вдоль биссектрис первого и второго квадрантов, поле (6.2) является подходящим. [17]
Начало координат является угловой точкой для графика этой функции, состоящей из биссектрис первого и второго координатных углов. [18]
Интересно отметить, что центр тяжести рассмотренной половины дуги кардиоиды лежит на биссектрисе первого координатное угла, хотя сама дуга и не симметрична относительно этой биссектрисы. [19]
Следует вычислить, площадь сектора, ограниченного линией, осью ординат н биссектрисой первого координатного утла. Эго дает ряд, быстро сходящийся. [20]
Найти координаты точки, симметричной точке А ( х, у) относительно биссектрисы первого ( второго) координатного угла. [21]
Какое соотношение существует между координатами точки, если она лежит: а) на биссектрисе первого и третьего координатных углов; б) на биссектрисе второго и четвертого координатных углов. [22]
Из сказанного делаем следующий практически важный вывод графики взаимно обратных функций расположены симметрично от мосительно биссектрисы первого — третьего координатных иглО ( ( черт. [23]
Найти координаты точки, симметричной точке А ( к, у) отн9 — сительно биссектрисы первого ( второго) координатного угла. [24]
Из сказанного делаем следующий практически важный вывод: графики взаимно обратных функций расположены симметрично относительно биссектрисы первого — третьего координатных углов ( черт. [25]
Возьмем две точки: Р0 и Рп / 2 — Они симметричны друг другу относительно биссектрисы первого и третьего координатных углов. [26]
Геометрический смысл этого предложения таков: линия у — х ( рис. 101) является биссектрисой первого и третьего координатных углов. Так как касательная к линии должна иметь в каждой своей точке то же самое направление, что и эта линия, то касательной к прямой линии в любой ее точке является она сама, и угловой коэффициент ее равен единице. [27]
Для того чтобы привести оси координат в привычное положение, повернем плоскость хОу на 180 вокруг биссектрисы первого и третьего координатных углов. [28]
Очевидно, что точки ( а; Ь) и ( Ь; а) симметричны относительно биссектрисы первого и третьего координатных углов. [29]
График обратной функции у р ( х) симметричен с графиком данной функции y fix) относительно биссектрисы первого и третьего координатных углов. [30]
УСЛОВИЕ:
4.2.30. Написать уравнение прямой, параллельной биссектрисе второго координатного угла и отсекающей на оси Оу отрезок, равный 3.
![]()
РЕШЕНИЕ ОТ SOVA ✪ ЛУЧШЕЕ РЕШЕНИЕ
Прямая у=- х — биссектриса второго и четвертого координатных углов.
Это следует из общего уравнения прямой у =kx+b
k- угловой коэффициент прямой
k=tg альфа,
альфа- угол, который образует прямая у= kx+b c положительным направлением оси Ох
b=0 — биссектриса проходит через начало координат
Параллельная ей прямая имеет вид
y=-x + с
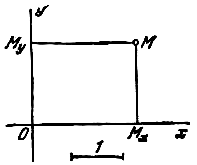
Так как по условию прямая отсекает на оси Оу отрезок, равный 3.
ОА=3
ОВ=3
см. рисунок
с = — 3 или с = 3
О т в е т. у= — х — 3 или у= — х + 3
Источник: http://sushi-vasabi.ru/bissektrisa-vtorogo-koordinatnogo-ugla/
Длина биссектрисы треугольника
Рассмотрим треугольник на Рис.5.
Длина биссектрисы треугольника можно вычислить следующими формулами:
где p − полупериметр треугольника ABC, ( small gamma -) угол между биссектрисой ( small l_c) и вершиной ( small h_c:)
Доказательство. 1) Из теоремы Стюарта следует:
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
Поскольку 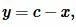 то (2) можно переписать так:
то (2) можно переписать так:
Найдем x из (3):
Тогда:
или
Подставим (4) и (5) в (1):
или
Cледовательно
Доказательство. 2) Подставим (4) и (5) в (6):
Тогда
Доказательство. 3) Сделаем следующее обозначение:
Сделаем преобразования формулы (7), учитывая (9):
Следовательно
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
Учитывая, что 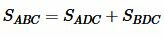 , получим:
, получим:
или
Тогда
Для ( small sin C ) применим формулу синуса двойного угла:
Подставляя (12) в (11) получим:
то есть
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
Тогда
Остается показать, что 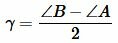 .
.
Поскольку биссектриса lc делит угол C пополам, то:
Далее
Тогда
Подставляя (14) в (15), получим:
или
Источник: http://matworld.ru/geometry/bissektrisa-treugolnika.php
ЧТО НЕОБХОДИМО знать и уметь
для успешного решения задач по геометрии?
От этого никуда не деться – чтобы наугад не тыкать носом кнопки, требуется освоить азы аналитической геометрии. Поэтому если вы только-только приступили к изучению геометрии или капитально позабыли её, пожалуйста, начните с урока Векторы для чайников. Кроме векторов и действий с ними, нужно знать базовые понятия геометрии плоскости, в частности, уравнение прямой на плоскости и простейшие задачи с прямой на плоскости. Геометрия пространства представлена статьями Уравнение плоскости, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость и некоторыми другими уроками. Кривые линии и пространственные поверхности второго порядка стоЯт некоторым особняком, и специфических задач с ними не так уж много.
Предположим, студент уже обладает элементарными знаниями и навыками решения простейших задач аналитической геометрии. Но вот бывает же так: читаешь условие задачи, и… хочется вообще закрыть всё это дело, закинуть в дальний угол и забыть, как о страшном сне. Причём это принципиально не зависит от уровня вашей квалификации, сам время от времени сталкиваюсь с заданиями, у которых решение не очевидно. Как поступать в таких случаях? Не нужно бояться задачи, которая вам не понятна!
Во-первых, следует установить – это «плоская» или пространственная задача? Например, если в условии фигурируют векторы с двумя координатами, то, понятно, тут геометрия плоскости. А если преподаватель загрузил благодарного слушателя пирамидой, то здесь явно геометрия пространства. Результаты первого шага уже неплохи, ведь удалось отсечь громадное количество ненужной для данной задачи информации!
Второе. Условие, как правило, озаботит вас некоторой геометрической фигурой. Действительно, пройдитесь по коридорам родного ВУЗа, и вы увидите очень много озабоченных лиц.
В «плоских» задачах, не говоря о разумеющихся точках и прямых, наиболее популярная фигура – треугольник. Его мы разберём очень подробно. Далее идёт параллелограмм, и значительно реже встречаются прямоугольник, квадрат, ромб, окружность, др. фигуры.
В пространственных задачах могут летать те же плоские фигуры + сами плоскости и распространённые треугольные пирамиды с параллелепипедами.
Вопрос второй – всё ли вы знаете о данной фигуре? Предположим, в условии идёт речь о равнобедренном треугольнике, а вы весьма смутно помните, что это такой за треугольник. Открываем школьный учебник и читаем про равнобедренный треугольник. Что делать… врач сказал ромб, значит, ромб. Аналитическая геометрия аналитической геометрией, но задачу помогут решить геометрические свойства самих фигур, известные нам из школьной программы. Если не знать, чему равна сумма углов треугольника, то мучиться можно долго.
Третье. ВСЕГДА старайтесь выполнять чертёж (на черновике/чистовике/мысленно), даже если этого не требуется по условию. В «плоских» задачах сам Евклид велел взять в руки линейку с карандашом – и не только для того, чтобы понять условие, но и в целях самопроверки. При этом наиболее удобный масштаб 1 единица = 1 см (2 тетрадные клетки). Уж не будем рассуждать о нерадивых студентах и вращающихся в гробах математиках – в таких задачах совершить ошибку практически невозможно. Для пространственных заданий выполняем схематический рисунок, который тоже поможет проанализировать условие.
Чертёж или схематический чертёж зачастую сразу позволяет увидеть путь решения задачи. Конечно, для этого нужно знать фундамент геометрии и рубить в свойствах геометрических фигур (см. предыдущий пункт).
Четвёртое. Разработка алгоритма решения. Многие задачи геометрии являются многоходовыми, поэтому решение и его оформление очень удобно разбивать на пункты. Нередко алгоритм сразу же приходит в голову, после того как вы прочитали условие или выполнили чертёж. В случае возникновения трудностей начинаем с ВОПРОСА задачи. Например, по условию «требуется построить прямую…». Здесь самый логичный вопрос такой: «А что достаточно знать, чтобы построить данную прямую?». Предположим, «точка нам известна, нужно знать направляющий вектор». Задаём следующий вопрос: «Как найти этот направляющий вектор? Откуда?» и т.д.
Иногда случается «затык» – не решается задача и всё тут. Причины стопора могут быть следующими:
– Серьёзный пробел в элементарных знаниях. Иными словами, вы не знаете или (и) не видите какой-то очень простой вещи.
– Незнание свойств геометрических фигур.
– Задача попалась трудная. Да, так бывает. Нет смысла часами париться и собирать слёзки в платочек. Обратитесь за консультацией к преподавателю, сокурсникам или задайте вопрос на форуме. Причём, его постановку лучше сделать конкретной – о том участке решения, который вам не понятен. Клич в виде «Как решить задачу?» выглядит не очень-то… и, прежде всего, для вашей собственной репутации.
Этап пятый. Решаем-проверяем, решаем-проверяем, решаем-проверяем-даём ответ. Каждый пункт задачи выгодно проверять сразу после его выполнения. Это поможет немедленно обнаружить ошибку. Естественно, никто не запрещает быстренько прорешать задачу целиком, но возникает риск переписывать всё заново (часто несколько страниц).
Вот, пожалуй, все основные соображения, которыми целесообразно руководствоваться при решении задач.
Практическая часть урока представлена геометрией на плоскости. Примеров будет всего два, но мало не покажется =)
Пройдёмся по нити алгоритма, который я только что рассмотрел в своём маленьком научном труде:
Пример 1
Даны три вершины  параллелограмма
параллелограмма  . Найти вершину
. Найти вершину  .
.
Начинаем разбираться:
Шаг первый: очевидно, что речь идёт о «плоской» задаче.
Шаг второй: в задаче речь идёт о параллелограмме. Все помнят такую фигуру параллелограмм? Не нужно улыбаться, немало людей получает образование в 30-40-50 и более лет, поэтому даже простые факты могут стереться из памяти. Определение параллелограмма встречается в Примере № 3 урока Линейная (не) зависимость векторов. Базис векторов.
Шаг третий: Выполним чертёж, на котором отметим три известные вершины. Забавно, что несложно сразу построить искомую точку  :
:

Построить, это, конечно, хорошо, но решение необходимо оформить аналитически.
Шаг четвёртый: Разработка алгоритма решения. Первое, что приходит в голову – точку  можно найти как пересечение прямых
можно найти как пересечение прямых  . Их уравнения нам неизвестны, поэтому придётся заняться этим вопросом:
. Их уравнения нам неизвестны, поэтому придётся заняться этим вопросом:
1) Противоположные стороны  параллельны. По точкам
параллельны. По точкам  найдём направляющий вектор данных сторон
найдём направляющий вектор данных сторон  . Это простейшая задача, которая рассматривалась на уроке Векторы для чайников.
. Это простейшая задача, которая рассматривалась на уроке Векторы для чайников.
Примечание: корректнее говорить «уравнение прямой, содержащей сторону», но здесь и далее для краткости я буду использовать словосочетания «уравнение стороны», «направляющий вектор стороны» и т.д.
2) Составим уравнение прямой  по известной точке
по известной точке  и найденному направляющему вектору
и найденному направляющему вектору  (см. статью Уравнение прямой на плоскости)
(см. статью Уравнение прямой на плоскости)
3) Противоположные стороны  параллельны. По точкам
параллельны. По точкам  найдём направляющий вектор этих сторон
найдём направляющий вектор этих сторон  .
.
4) Составим уравнение прямой  по точке
по точке  и направляющему вектору
и направляющему вектору 
В пунктах 1-2 и 3-4 мы фактически дважды решили одну и ту же задачу, она, кстати, разобрана в примере № 3 урока Простейшие задачи с прямой на плоскости. Можно было пойти более длинным путём – сначала найти уравнения прямых  и только потом «вытащить» из них направляющие векторы
и только потом «вытащить» из них направляющие векторы  .
.
5) Теперь уравнения прямых  известны. Осталось составить и решить соответствующую систему линейных уравнений (см. примеры № 4, 5 того же урока Простейшие задачи с прямой на плоскости).
известны. Осталось составить и решить соответствующую систему линейных уравнений (см. примеры № 4, 5 того же урока Простейшие задачи с прямой на плоскости).
Точка  найдена.
найдена.
Задача довольно таки простая и её решение очевидно, но существует более короткий путь!
Второй способ решения:
Диагонали параллелограмма своей точкой пересечения делятся пополам. Точку  я отметил, но чтобы не загромождать чертёж сами диагонали не провёл.
я отметил, но чтобы не загромождать чертёж сами диагонали не провёл.
1) С помощью формул координат середины отрезка найдём точку  – середину диагонали
– середину диагонали  .
.
2) Рассмотрим диагональ  . Из условия известна вершина «бэ», из предыдущего пункта найдена середина
. Из условия известна вершина «бэ», из предыдущего пункта найдена середина  . Используя те же формулы координат середины отрезка, находим вершину
. Используя те же формулы координат середины отрезка, находим вершину  .
.
Хорошее знание свойств параллелограмма позволило значительно сократить решение!
Желающие могут прорешать задачу. Всё перед глазами, все ссылки, комментарии даны. И, конечно, не забывайте про важный технический приём – решили пункт задания и сразу же его проверили (аналитически или по чертежу).
Переходим к наиболее распространённой задаче, которая встречается практически в каждом сборнике, в каждой методичке:
Источник: http://mathprofi.ru/kak_nauchitsa_reshat_zadachi_po_geometrii.html
Основное свойство биссектрисы угла
На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:
Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.
В переводе с математического на русский это означает сразу два факта:
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:
Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.
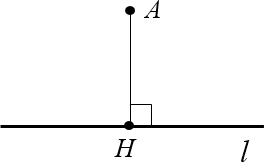 Графическое представление расстояния от точки до прямой
Графическое представление расстояния от точки до прямой
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:
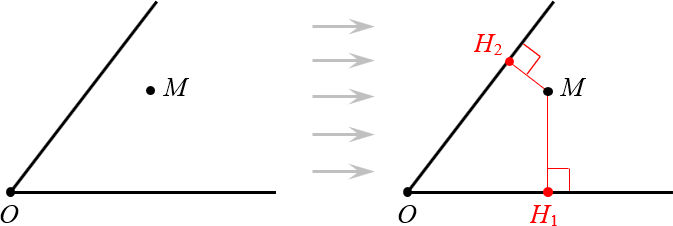 Определяем расстояние от точки до сторон угла
Определяем расстояние от точки до сторон угла
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.
Как и обещал, разобьём доказательство на две части:
1. Расстояния от точки на биссектрисе до сторон угла одинаковы
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:
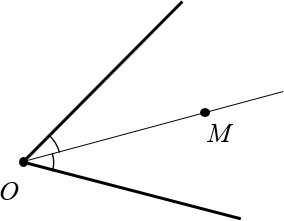
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:
Провели перпендикуляры к сторонам угла
Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:
- $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
- $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
- $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)
2. Если расстояния равны, то точка лежит на биссектрисе
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:
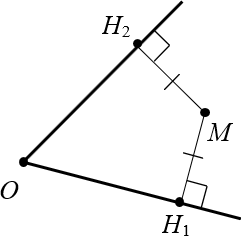
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.
Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:
Провели луч $OM$ внутри угла
Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:
- Гипотенуза $OM$ — общая;
- Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
- Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.
Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.
В заключение доказательства отметим красными дугами образовавшиеся равные углы:
Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных
Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)
Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.
Смотрите также:
- Высота в треугольнике

- Основное свойство биссектрисы угла в треугольнике и его применение для решения задач

- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)

- Правила вычисления производных

- Сводный тест по задачам B15 (2 вариант)

- Симметрия корней и оптимизация ответов в тригонометрии

Источник: http://berdov.com/docs/treugolnik/bissektrisa-ugla/
Делящая пополам угол линия
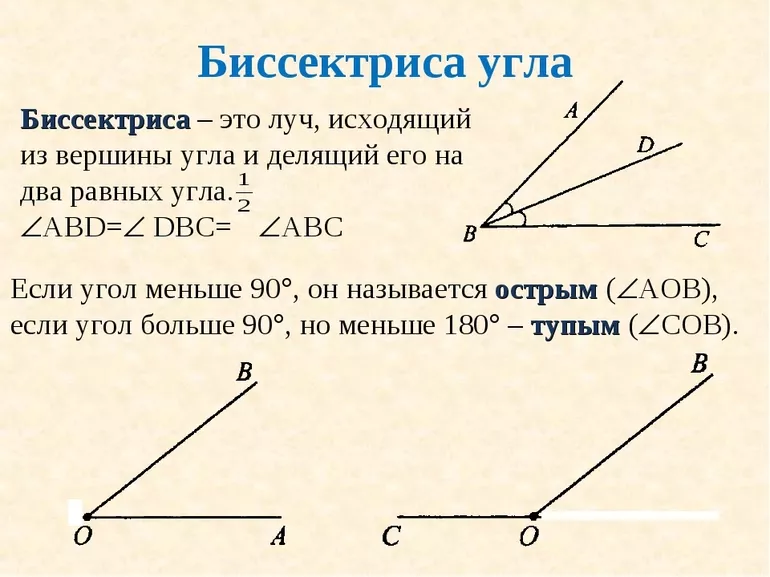
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
- С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
- С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
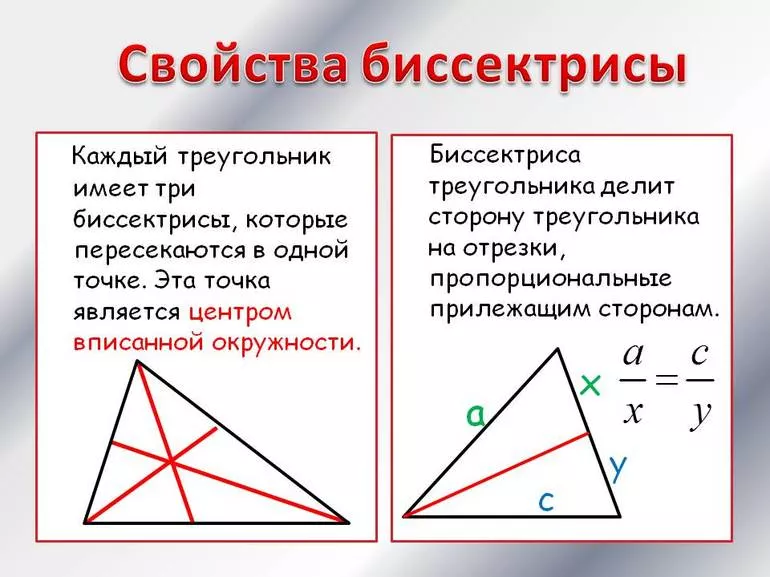
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
DB/DC = AB/AC.

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
L (A) = 2/(b+c)*(b*c*p*(p-a))^0,5.
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Источник: http://nauka.club/matematika/geometriya/uravnenie-bissektrisy-v-treugolnike.html
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

- Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
- Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
- Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.
Источник: http://nauka.club/matematika/geometriya/uravnenie-bissektrisy-v-treugolnike.html