Длина дуги параболы

Как с помощью интеграла найти длину дуги кривой, заданной в прямоугольных координатах, параметрически и в полярных координатах

[править] Обозначения

Введём обозначения:

x1 — абсцисса первой точки дуги;

y1 — ордината (меньшая) первой точки дуги;

x2 — абсцисса второй точки дуги;

y2 — ордината (большая) второй точки дуги;

y2 = 2px — каноническое уравнение параболы;

Lдуг.пар — длина дуги параболы.

Источник: http://cyclowiki.org/wiki/Длина_дуги_параболы

Как найти длину дуги кривой, если линия задана параметрически?

Если линия задана параметрическими уравнениями 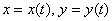, то при выполнении некоторых условий, на которых я не буду останавливаться, длина дуги кривой 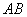, которая прочерчивается при изменении параметра в пределах 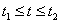, рассчитывается по формуле:

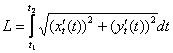, где

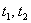– значения, определяющие точк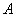и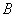

В начале урока о площади и объёме при линиях, заданных параметрически, я обратил ваше внимание на тот факт, что параметрические уравнения могут «прорисовывать» кривую 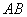как слева направо, так и справа налево, из-за чего во втором случае «вылезает минус» и возникают небольшие технические затруднения. В рассматриваемой задаче мы от этого избавлены! Так как подынтегральная функция, как и в первом пункте, неотрицательна 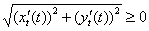, то заранее можно утверждать, что результата со знаком «минус» получиться не должно (понятно, при условии ).

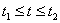Однако вместо «вопроса прорисовки дуги» у нас появляется другая почётная обязанность – беречь неотрицательность подынтегральной функции, как зеницу ока:

Пример 4

Вычислить длину дуги кривой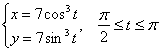

Решение: аналитические условия задают левую верхнюю дугу астроиды. Причём параметрические уравнения «прорисовывают» эту кривую справа налево, но, как я только что отметил, сейчас нас это не волнует, и асфальтный каток едет дальше.

Используем формулу .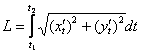

Сначала найдём производные:

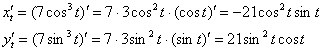
и упростим сумму их квадратов:

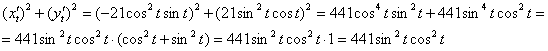
Это оптимальная во многих случаях техника решения, позволяющая не «таскать за собой» значки корня и интеграла с пределами интегрирования. Тем самым минимизируется риск что-нибудь потерять в громоздкой записи.

Гораздо удобнее «зарядить» в формулу готовую сумму:

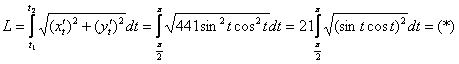
А вот теперь самый важный момент. Здесь нельзя «машинально» избавляться от корня и необходимо придерживаться следующего правила:

, если функция на промежутке ,
или , если на данном промежутке.

Эта «развилка» сохраняет неотрицательность подынтегральной функции, что соответствует геометрическому смыслу задачи.

На отрезке , следовательно, их произведение неположительное: и поэтому

Не понимаете, почему ? Посмотрите на их графики.

Продолжаем, а точнее, заканчиваем решение:

Ответ:

Приятно, когда знаешь график функции, но вдвойне приятнее, когда можно эффективно проверить или даже заранее узнать ответ. Длина астроиды 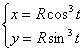равна . В нашей задаче и мы рассчитали длину «четвертинки»:

, что и требовалось проверить.

Тренируемся самостоятельно:

Пример 5

Вычислить длину дуги кривой с точностью до двух знаков после запятой

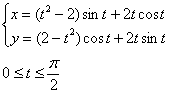
Примерный образец оформления задачи и в конце урока.

Продолжаем динамично закатывать асфальт:

Источник: http://mathprofi.ru/dlina_dugi_krivoi.html

Как узнать, что перед нами уравнение параболы?

Если определения из учебника кажутся сложными, можно запомнить так:
Парабола – это график КВАДРАТичной функции.
Уравнение квадратичной функции выглядит почти так же, как квадратное уравнение:

Т.е. самая большая степень икса — вторая.

Оно может быть полным или неполным, но всегда содержит Х².

Источник: http://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/parabola-vse-chto-nujno-znat-o-funkcii-5ff12009fe4e686f6a364945

[править] Формула

[math]L_text{дуг.пар}=frac{y_2sqrt{y_2^2+p^2}-y_1sqrt{y_1^2+p^2}}{2p}+frac{p}{2}lnleft|frac{y_2sqrt{y_2^2+p^2}}{y_1sqrt{y_1^2+p^2}}right| Leftrightarrow[/math][math]Leftrightarrow L_text{дуг.пар}=frac{y_2sqrt{2px_2+p^2}-y_1sqrt{2px_1+p^2}}{2p}+frac{p}{2}lnleft|frac{y_2sqrt{2px_2+p^2}}{y_1sqrt{2px_1+p^2}}right| Leftrightarrow[/math][math]Leftrightarrow L_text{дуг.пар}= sign y_2sqrt{x_2}sqrt{x_2+frac{p}{2}}-sign y_1sqrt{x_1}sqrt{x_1+frac{p}{2}}+frac{p}{2}lnleft|frac{sign y_2sqrt{x_2}+sqrt{x_2+frac{p}{2}}}{sign y_1sqrt{x_1}+sqrt{x_1+frac{p}{2}}}right|[/math]

Заметим, что формула верна для точек с положительными и отрицательными ординатами, причём y2 > y1.

Источник: http://cyclowiki.org/wiki/Длина_дуги_параболы

[править] Другие формулы

длина дуги плоской кривой;
длина дуги окружности;
длина дуги параболы;
длина дуги эллипса;
длина дуги гиперболы;
длина дуги синусоиды;
длина дуги косинусоиды;
длина дуги циклоиды;
длина дуги кардиоиды;
длина дуги астроиды;
длина дуги эпициклоиды;
длина дуги гипоциклоиды;
длина дуги эвольвенты окружности;
длина дуги цепной линии;
длина дуги трактрисы;
длина дуги лемнискаты Бернулли.

Источник: http://cyclowiki.org/wiki/Длина_дуги_параболы

[править] Ссылки

Участник:Logic-samara

Источник: http://cyclowiki.org/wiki/Длина_дуги_параболы

Смотрите также

Дуга (геометрия)
Длина окружности
Формула Крофтона
Эллиптический интеграл
Геодезические
Внутреннее уравнение
Интегральные приближения
Линейный интеграл
Дуга меридиана
Многопараметрическое исчисление
Извилистость

Источник: http://ru.qaz.wiki/wiki/Arc_length

Источники

Фаруки, Рида Т. (1999). «Кривые от движения, движение от кривых». В Laurent, P.-J .; Sablonniere, P .; Шумакер, LL (ред.). Кривая и дизайн поверхностей: Сен-Мало 1999 . Vanderbilt Univ. Нажмите. С. 63–90. ISBN 978-0-8265-1356-4.

Источник: http://ru.qaz.wiki/wiki/Arc_length

Внешние ссылки

«Спрямляемая кривая» , Энциклопедия математики , EMS Press , 2001 [1994]
История искривления
Вайсштейн, Эрик В. «Длина дуги» . MathWorld .
Длина дуги , Эд Пегг младший , Демонстрационный проект Вольфрама , 2007.
Учебное пособие по исчислению — Длина дуги (выпрямление)
Указатель известных кривых Архив истории математики MacTutor
Аппроксимация длины дуги, сделанная Чадом Пирсоном, Джошем Фрицем и Анжелой Шарп, The Wolfram Demonstrations Project .
Длина кривой. Эксперимент. Иллюстрирует численное решение нахождения длины кривой.

Источник: http://ru.qaz.wiki/wiki/Arc_length