Вычисление производной в Excel методом численного дифференцирования с помощью конечных разностей. Практический пример вычисления производной второго порядка.
Минимум теории.
Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.
Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.
y’(x)=lim (Δy/Δx) при Δx→0
Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.
tg (α)=Δy/Δx
Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.
y’(x)i≈(Δy/Δx)i=(yi+1—yi-1)/(xi+1—xi-1)
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.


Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Источник: http://al-vo.ru/spravochnik-excel/vychislenie-proizvodnoj-v-excel.html
 WHOIS – проверка домена
WHOIS – проверка домена
 Expired.ru
Expired.ru
Список освобождающихся доменов в зоне .RU и .РФ, сервис перехвата доменов. Заявка на регистрацию домена подается через максимально возможный пул регистраторов, что значительно увеличивает ваши шансы.
Источник: http://uchi24.ru/rezhissery-prodyusery/naiti-proizvodnuyu-funkcii-v-eksel-graficheskoe-i-chislennoe-differencirovanie-algoritm-postroeniya-g/
Вычисление производной в Excel
 Чем может помочь Excel при вычислении производной функции? Если функция задана уравнением, то после аналитического дифференцирования и получения формулы Excel поможет быстро рассчитать значения производной для любых интересующих пользователя значений аргумента.
Чем может помочь Excel при вычислении производной функции? Если функция задана уравнением, то после аналитического дифференцирования и получения формулы Excel поможет быстро рассчитать значения производной для любых интересующих пользователя значений аргумента.
Если функция получена практическими измерениями и задана табличными значениями, то Excel может оказать в этом случае более существенную помощь при выполнении численного дифференцирования и последующей обработке и анализе результатов.
На практике задача вычисления производной методом численного дифференцирования может возникнуть и в механике (при определении скорости и ускорения объекта по имеющимся замерам пути и времени) и в теплотехнике (при расчете теплопередачи во времени). Это также может быть необходимо, например, при бурении скважин для анализа плотности проходимого буром слоя грунта, при решении целого ряда баллистических задач, и т. д.
Похожая ситуация имеет место при «обратной» задаче расчета сложно нагруженных балок, когда по прогибам возникает желание найти значения действующих нагрузок.
Во второй части статьи на «живом» примере рассмотрим вычисление производной по приближенной формуле численного дифференцирования с применением выражений в конечных разностях и разберемся в вопросе – можно ли используя приближения производных конечными разностями по прогибам балки определять действующие в сечениях нагрузки?
Источник: http://stroynietela.ru/kak-sdelat-proizvodnuyu-v-eksele/
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
Дано:
На балку длиной 8 метров с шарнирными опорами по краям изготовленную из двух спаренных стальных (Ст3) двутавров 30М опираются 7 прогонов с шагом 1 метр. К центральной части балки крепится площадка с оборудованием. Предположительно усилие от покрытия, передаваемое через прогоны на балку, во всех точках одинаково и равно F1. Подвесная площадка имеет вес 2*F2 и крепится к балке в двух точках.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.

На следующем скриншоте представлены исходные данные.

Расчетные исходные данные:
3. Погонная масса двутавра 30М:
γ=50,2 кг/м
Сечение балки составлено из двух двутавров:
n=2
Удельный вес балки:
q=γ*n*g=50,2*2*9,81/1000=0,985 Н/мм
5. Момент инерции сечения двутавра 30М:
Ix1=95 000 000 мм4
Момент инерции составного сечения балки:
Ix=Ix1*n=95 000 000*2=190 000 000 мм4
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R=(q*zmax+8*F1+2*F2)/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
В расчете учитывается собственный вес балки!
Задача:
Найти значения изгибающего момента Mxi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Qy, изгибающих моментов Mx, углов поворота Ux оси балки и прогибов Vx по классическим формулам сопромата во всех сечениях с шагом h. (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.

Использованные в расчетах формулы можно посмотреть здесь.
Ссылка для скачивания файла с рассмотренным в статье примером: vychisleniye-proizvodnoy (xls 250,0KB).
Итак, нам известны точные значения моментов и прогибов.
Из теории мы знаем, что:
Угол поворота – это первая производная прогиба U=V’.
Момент – это вторая производная прогиба M=V’’.
Сила – это третья производная прогиба Q=V’’’.
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Mxi=Vy’’≈((Vi+1-2*Vi+Vi-1)/h2)*E*Ix
Итог расчетов мы видим в ячейках M5-M54.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
ε=(Mx—Vy’’)/Mx*100%
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Источник: http://al-vo.ru/spravochnik-excel/vychislenie-proizvodnoj-v-excel.html
Метод касательных
Метод касательных основан на геометрической интерпретации производной. При использовании метода кинематических диаграмм вначале дифференцируется диаграмма перемещений для получения графика (диаграммы) скоростей. Рассмотрим графическое дифференцирование на этом примере.
V = ds/dt, но т.к. аналитическое выражение для перемещений в данном случае отсутствует, то представляем значения перемещений и времени через отрезки на диаграмме перемещений:
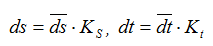
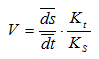
Но отношение бесконечно малого приращения функции к бесконечно малому приращению аргумента на графике представляет собой тангенс угла наклона касательной к данной кривой в рассматриваемой точке, т.е.
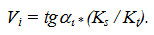
Используя данное обстоятельство, диаграмму скоростей строят в следующем порядке (рисунок 11):
- проводят касательные к диаграмме перемещений в намеченных положениях;
- слева от начала координат на оси абсцисс будущей диаграммы скоростей отмечают полюс P на некотором расстоянии H (которое называется полюсным расстоянием);
- из полюса проводят лучи, параллельные проведенным касательным на диаграмме перемещений. Эти лучи отсекают на оси ординат будущей диаграммы скоростей отрезки
Таким образом, и скорость в i-том положении и отрезки oi* пропорциональны tgαi , а значит отрезки oi* пропорциональны Vi (скорости исследуемого звена в соответствующем положении механизма), т.е. они представляют собой изображение скорости в виде отрезка в некотором масштабе – Vi.
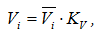
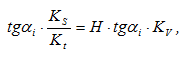
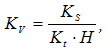
где Kv – масштаб диаграммы скоростей по оси ординат в (м/с)/мм.
Далее отрезки oi* переносят в соответствующие положения, отмеченные на оси абсцисс, и, соединив концы отрезков плавной кривой, получают диаграмму скоростей исследуемого звена. Аналогично строится диаграмма ускорений. При этом масштаб ускорений
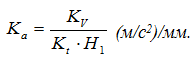
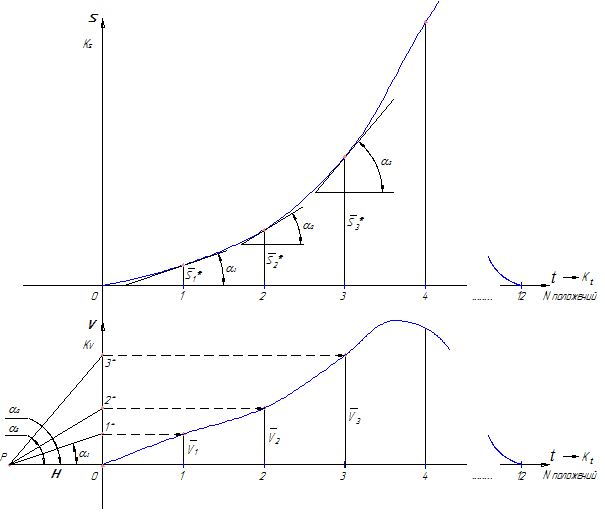
Теоретически метод касательных самый точный из графических методов дифференцирования, т.к. дает значение мгновенной скорости (ускорения) именно в том положении, в котором проведена касательная.
Однако из-за трудности точного проведения касательных (и сама дифференцируемая кривая, построенная по точкам, имеет отклонения от ее теоретической функции), практическая точность этого метода весьма низкая, поэтому он используется редко (обычно когда надо проанализировать характер движения звена без получения конкретных численных результатов).
Источник: http://rg-gaming.ru/kompjutery/graficheskoe-differencirovanie-v-excel
Однако…
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.

Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε21=1,813%).
Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Уважаемые читатели, отзывы и комментарии к статье, размещайте в специальном блоке ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге, подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл с примером ПОСЛЕ ПОДПИСКИ на анонсы статей.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Источник: http://al-vo.ru/spravochnik-excel/vychislenie-proizvodnoj-v-excel.html