Дробное преобразование Фурье

This MATLAB function computes the discrete Fourier transform (DFT) of X using a fast Fourier transform (FFT) algorithm.

4 ответов

1) Почему ось x (частота) заканчивается на 500? Откуда мне знать, что частот больше нет или они просто игнорируются?

Он заканчивается на 500Hz, потому что это частота Найквиста сигнала когда образец на 1000Hz. Посмотрите на эту строку в Примере Mathworks:

f = Fs/2*linspace(0,1,NFFT/2+1);

ось частоты второго графика идет от 0 до Fs / 2, или половина частоты дискретизации.Частота Найквиста всегда половина частота дискретизации, потому что выше этого, псевдоним происходит: 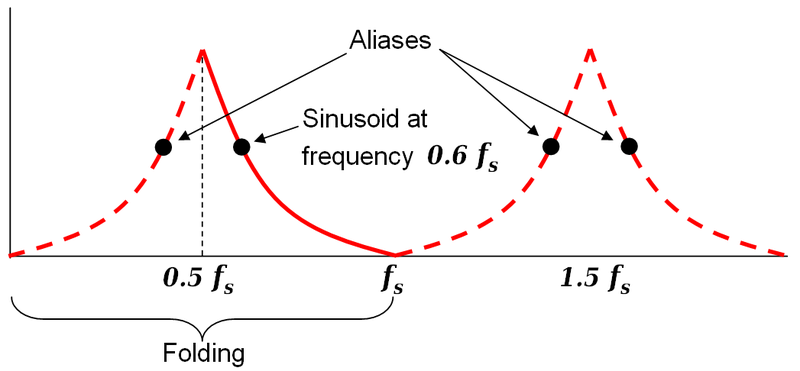Aliasing illustration

сигнал будет «складываться» обратно на себя, и появляется некоторые частоты ниже 500Гц.

2) Как узнать, что частоты находятся между 0 и 500? Разве БПФ не должен сказать мне, в каких пределах частоты?

из-за» складывания», описанного выше (частота Найквиста также широко известна как» частота складывания»), это физически невозможно, чтобы частоты выше 500 Гц появлялись в БПФ; более высокие частоты будут «складываться» назад и появляться как более низкие частоты.

возвращает ли БПФ только значение амплитуды без частоты?

да, функция MATLAB FFT возвращает только один вектор амплитуд. Однако сопоставление частотных точек, вы передаете ей.

Дайте мне знать, что нуждается в разъяснении, чтобы я мог помочь вам дальше.

здесь есть некоторые заблуждения.

частоты выше 500 can быть представленным в результате БПФ длины 1000. К сожалению, эти частоты все сложены вместе и смешаны в первые 500 БПФ результат бункеров. Поэтому обычно вы не хотите подавать БПФ сигнал, содержащий какие-либо частоты на или выше половины частоты дискретизации, поскольку БПФ не будет заботиться и будет просто смешивать высокие частоты вместе с низкими (сглаживание), что делает результат довольно много бесполезных. Вот почему данные должны быть отфильтрованы с низким пропуском перед выборкой и подачей в БПФ.

БПФ возвращает амплитуды без частот, потому что частоты зависят не только от длины БПФ, но и от частоты дискретизации данных, которая не является частью самого БПФ или его ввода. Вы можете подавать данные БПФ одинаковой длины при любой частоте дискретизации, так как таким образом получите из него любой диапазон частот.

причина результирующие эпюры заканчивается на 500, что для любой реальный ввод данных, частоты выше половины длины БПФ являются просто зеркальными повторами (комплексно сопряженными) данных в первой половине. Поскольку они дубликаты, большинство людей просто игнорируют их. Почему дублирует сюжет? БПФ вычисляет другую половину результата для людей, которые кормят сложные данные БПФ (как с реальными, так и с воображаемыми компонентами), что создает две разные половины.

похоже, вам нужно какое-то фоновое чтение о том, что такое БПФ (например,http://en.wikipedia.org/wiki/FFT). Но чтобы ответить на ваши вопросы:

Почему ось x (частота) заканчивается на 500?

потому что входной вектор имеет длину 1000. В общем, БПФ длины -N входной сигнал приведет к длине -N выходной вектор. Если форма входного сигнала реальна, то выход будет симметричен, поэтому достаточно первых 501 очка.

Edit: (Я не заметил, что пример дополняет вектор временной области.)

частота идет к 500 Hz потому что объявлена, что имеет форма волны врем-домена частоту дискретизации 1 кГц. Теорема выборки Найквиста диктует, что сигнал с частотой дискретизации fs может поддерживать (реальный) сигнал с максимальной пропускной способностью fs/2.

откуда я знаю, что частоты между 0 и 500?

см. выше.

не должен ли БПФ сказать мне, в каких пределах находятся частоты?

нет.

возвращает ли БПФ только значение амплитуды без частоты?

БПФ просто назначает амплитуду (и фазу) для каждого частотного Бина.

автор: Oliver Charlesworth

причина, по которой ваша ось X отображает частоты только до 500 Гц, — это ваша команда ‘ f = Fs/2*linspace(0,1,NFFT / 2+1);’. Ваш Fs-1000. Поэтому, когда вы делите его на 2 , а затем умножаете на значения от 0 до 1, он возвращает вектор длины NFFT/2+1. Этот вектор состоит из равномерно разнесенных значений частоты в диапазоне от 0 до Fs / 2 (т. е. 500 Гц). Так как вы заговор с использованием’ участок (f, 2 * abs (Y (1: NFFT / 2+1))))‘ команда, ваш предел оси X составляет 500 Гц.

Источник: http://askdev.ru/q/ponimanie-primera-fft-matlab-67956/

Исследование простейших радиотехнических сигналов, разложение их в ряд Фурье. Построение амплитудных спектров синуса, суммы синусов и синка. Создание в среде программирования Matlab программ с параметрами: длина сигнала, амплитуда, частота дискретизации.

Лабораторная работа № 2

по дисциплине «Сигналы и процессы в радиотехнике»

Преобразование Фурье в MATLAB

Целью данной работы является изучение простейших радиотехнических сигналов, разложение их в ряд Фурье, создание в среде программирования Matlab соответствующих программ.

Задание №1.

Синус

Листинг программы

clear all% Очистка памяти

% Параметры

Tm = 5;% Длина сигнала (с)

Fd = 512;% Частота дискретизации (Гц)

A1 = 2;% Амплитуда синусоиды

F1 = 0.01;% Частота синусоиды (Гц)

Phi1 = 0;% Начальная фаза синусоиды

FftL = 1024;% Количество линий Фурье спектра

T = 0:1/Fd:Tm;% Массив отсчетов времени

Signal = A1*sin(F1*360.*T+Phi1);% Массив сигнала

% Спектральное представление сигнала

FftS = abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала

FftS = 2*FftS./FftL;% Нормировка спектра по амплитуде

F = 0:Fd/FftL:Fd/2-Fd/FftL;% Массив частот вычисляемого спектра Фурье

% Построение графиков

figure(1)% Создаем новое окно

plot(T, Signal);% Построение сигнала

title(‘Сигнал’);% Подпись графика

xlabel(‘Время (с)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

figure(2)% Создаем новое окно

plot(F, FftS(1:length(F)));% Построение спектра Фурье сигнала

title(‘Спектр сигнала’);% Подпись графика

xlabel(‘Частота (Гц)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

Рисунок 1 Исследуемый сигнал

Рисунок 2 Амплитудный спектр исследуемого сигнала

Задание №2

Сумма синусов

Листинг программы

clear all;% Очистка памяти

% Параметры

Tm = 5;% Длина сигнала (с)

Fd = 512;% Частота дискретизации (Гц)

A1 = 2;% Амплитуда первой синусоиды

A2 = 3;% Амплитуда второй синусоиды

F1 = 0.1;% Частота первой синусоиды (Гц)

F2 = 0.2;% Частота второй синусоиды (Гц)

Phi1 = 0;% Начальная фаза первой синусоиды

Phi2 = 2;% Начальная фаза второй синусоиды

FftL = 5120;% Количество линий Фурье спектра

T = 0:1/Fd:Tm;% Массив отсчетов времени

Signal = A1*sin(F1*360.*T+Phi1)+A2*sin(F2*360.*T+Phi2);% Массив сигнала

% Спектральное представление сигнала

FftS = abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала

FftS = 2*FftS./FftL;% Нормировка спектра по амплитуде

F = 0:Fd/FftL:Fd/2-Fd/FftL;% Массив частот вычисляемого спектра Фурье

% Построение графиков

figure(1)% Создаем новое окно

plot(T, Signal);% Построение сигнала

title(‘Сигнал’);% Подпись графика

xlabel(‘Время (с)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

figure(2)% Создаем новое окно

plot(F, FftS(1:length(F)));% Построение спектра Фурье сигнала

title(‘Спектр сигнала’);% Подпись графика

xlabel(‘Частота (Гц)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

Рисунок 3 Исследуемый сигнал

Рисунок 4 Амплитудный спектр исследуемого сигнала

Задание №3

Синк

Листинг программы

clear all% Очистка памяти

% Параметры

Tm = 5;% Длина сигнала (с)

Fd = 512;% Частота дискретизации (Гц)

A1 = 2;% Амплитуда

F1 = 0.01;% Частота (Гц)

Phi1 = 0;% Начальная фаза

FftL = 512000;% Количество линий Фурье спектра

T = -Tm:1/Fd:Tm;% Массив отсчетов времени

Signal = A1*sinc(F1*360.*T+Phi1);% Массив сигнала

% Спектральное представление сигнала

FftS = abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала

F = 0:Fd/FftL:Fd/2-Fd/FftL;% Массив частот вычисляемого спектра Фурье

% Построение графиков

figure(1)% Создаем новое окно

plot(T, Signal);% Построение сигнала

title(‘Сигнал’);% Подпись графика

xlabel(‘Время (с)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

figure(2)% Создаем новое окно

plot(F, FftS(1:length(F)));% Построение спектра Фурье сигнала

axis([0,5,0,1000]);% Граници спектра

title(‘Спектр сигнала’);% Подпись графика

xlabel(‘Частота (Гц)’);% Подпись оси х графика

ylabel(‘Амплитуда’);% Подпись оси у графика

Рисунок 5 Исследуемый сигнал

Рисунок 6 Амплитудный спектр исследуемого сигнала

сигнал амплитуда спектр

Вывод

Я исследовал сигналы в программе MATLAB. Спектр синуса имеет один пик в амплитудном спектре, сумма синусов — два пика, синк имеет спектр в виде прямоугольного импульса. У периодических сигналов спектр — линейчатый, а у не периодического — сплошной. При увеличении периода сигнала — ширина ?w между спектральными линиями увеличивается, и наоборот при уменьшении периода — ширина ?w — уменьшается. Для получения не периодического сигнала необходимо период устремить к бесконечности, в этом случае копия сигнала будет отсутствовать. Если разложить сигнал в ряд Фурье (тригонометрический), то мы получим АЧХ и ФЧХ представления сигналов.

Источник: http://stud.wiki/programming/2c0a65635a3ac79b5d53a88421316c37_0.html

Вступление

Непрерывное преобразование Фурье от функции ƒ: R → C является унитарным оператором из L 2 , который отображает функцию ƒ своей версию ƒ частотной (все выражения берутся в L 2 смысла, а не точечно): F { Displaystyle { mathcal {F}}} ${ mathcal {F}}$

ж ^ ( ξ ) знак равно ∫ — ∞ ∞ ж ( Икс ) е — 2 π я Икс ξ d Икс { displaystyle { hat {f}} ( xi) = int _ {- infty} ^ { infty} f (x) e ^ {- 2 pi ix xi} , mathrm {d } Икс} ${ hat {f}} ( xi) = int _ {- infty} ^ { infty} f (x) e ^ {- 2 pi ix xi} , mathrm {d} x$

а ƒ определяется через обратное преобразование F — 1 { Displaystyle { mathcal {F}} ^ {- 1}} ${ mathcal {F}} ^ {- 1}$

ж ( Икс ) знак равно ∫ — ∞ ∞ ж ^ ( ξ ) е 2 π я ξ Икс d ξ , { Displaystyle е (х) = int _ {- infty} ^ { infty} { hat {f}} ( xi) e ^ {2 pi i xi x} , mathrm {d } xi,}

$f (x) = int _ {- infty} ^ { infty} { hat {f}} ( xi) e ^ {2 pi i xi x} , mathrm {d} xi ,$

Давайте изучим его n -ю итерацию, определенную посредством и, когда n — неотрицательное целое число, и . Их последовательность конечна , поскольку представляет собой 4-периодический автоморфизм : для каждой функции ƒ, . F п { Displaystyle { mathcal {F}} ^ {п}} ${ mathcal {F}} ^ {n}$ F п [ ж ] знак равно F [ F п — 1 [ ж ] ] { displaystyle { mathcal {F}} ^ {n} [f] = { mathcal {F}} [{ mathcal {F}} ^ {n-1} [f]]} ${ mathcal {F}} ^ {n} [f] = { mathcal {F}} [{ mathcal {F}} ^ {n-1} [f]]$ F — п знак равно ( F — 1 ) п { displaystyle { mathcal {F}} ^ {- n} = ({ mathcal {F}} ^ {- 1}) ^ {n}} ${ mathcal {F}} ^ {- n} = ({ mathcal {F}} ^ {- 1}) ^ {n}$ F 0 [ ж ] знак равно ж { displaystyle { mathcal {F}} ^ {0} [f] = f} ${ mathcal {F}} ^ {0} [f] = f$ F { Displaystyle { mathcal {F}}} ${ mathcal {F}}$ F 4 [ ж ] знак равно ж { displaystyle { mathcal {F}} ^ {4} [f] = f} ${ mathcal {F}} ^ {4} [f] = f$

Точнее, введем оператор четности , который переворачивает , . Тогда имеют место следующие свойства: п { displaystyle { mathcal {P}}} ${ mathcal {P}}$ Икс { displaystyle x} $Икс$ п [ ж ] : Икс ↦ ж ( — Икс ) { Displaystyle { mathcal {P}} [е] двоеточие x mapsto f (-x)} ${ Displaystyle { mathcal {P}} [е] двоеточие x mapsto f (-x)}$

F 0 знак равно я d , F 1 знак равно F , F 2 знак равно п , F 4 знак равно я d { Displaystyle { mathcal {F}} ^ {0} = mathrm {Id}, qquad { mathcal {F}} ^ {1} = { mathcal {F}}, qquad { mathcal {F }} ^ {2} = { mathcal {P}}, qquad { mathcal {F}} ^ {4} = mathrm {Id}} ${ mathcal {F}} ^ {0} = mathrm {Id}, qquad { mathcal {F}} ^ {1} = { mathcal {F}}, qquad { mathcal {F}} ^ {2} = { mathcal {P}}, qquad { mathcal {F}} ^ {4} = mathrm {Id}$ F 3 знак равно F — 1 знак равно п ∘ F знак равно F ∘ п . { Displaystyle { mathcal {F}} ^ {3} = { mathcal {F}} ^ {- 1} = { mathcal {P}} circ { mathcal {F}} = { mathcal {F }} circ { mathcal {P}}.} ${ mathcal {F}} ^ {3} = { mathcal {F}} ^ {- 1} = { mathcal {P}} circ { mathcal {F}} = { mathcal {F}} круг { mathcal {P}}.$

FRFT предоставляет семейство линейных преобразований, которое дополнительно расширяет это определение для обработки нецелочисленных степеней n = 2 α / π FT.

Источник: http://ru.other.wiki/wiki/Fractional_Fourier_transform

Преобразование Лапласа

Преобразование Лапласа функции времени f (t) задается следующим интегралом:

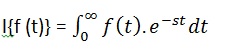
Преобразование Лапласа

Преобразование Лапласа также обозначается как преобразование f (t) в F (s). Вы можете видеть, что этот процесс преобразования или интеграции преобразует функцию f (t) символической переменной t в другую функцию F (s) с другой переменной s.

Преобразование Лапласа превращает дифференциальные уравнения в алгебраические. Чтобы вычислить преобразование Лапласа функции f (t), напишите —

laplace(f(t))

пример

В этом примере мы вычислим преобразование Лапласа некоторых часто используемых функций.

Создайте файл сценария и введите следующий код —

syms s t a b wlaplace(a)laplace(t^2)laplace(t^9)laplace(exp(-b*t))laplace(sin(w*t))laplace(cos(w*t))

Когда вы запускаете файл, он показывает следующий результат —

ans = 1/s^2ans = 2/s^3ans = 362880/s^10ans = 1/(b + s) ans = w/(s^2 + w^2) ans = s/(s^2 + w^2)

Источник: http://coderlessons.com/tutorials/kompiuternoe-programmirovanie/uznaite-matlab/matlab-preobrazovaniia

Ссылки

В статье на википедии можно прочитать о скорости работы алгоритма.
Описание функции fft и пример в докментации matlab.

Источник: http://theor.mephi.ru/wiki/index.php?title=Быстрое_преобразование_Фурье

Некоторые применения

Помимо непосредственного применения для перемножения многочленов или длинных чисел, опишем здесь некоторые другие приложения дискретного преобразования Фурье.

Всевозможные суммы

Задача: даны два массива a[] и b[] . Требуется найти всевозможные числа вида a[i]+b[j] , и для каждого такого числа вывести количество способов получить его.

Например, для a = (1,2,3) и b = (2,4) получаем: число 3 можно получить 1 способом, 4 — также одним, 5 — 2, 6 — 1, 7 — 1.

Построим по массивам и два многочлена и 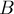. В качестве степеней в многочлене будут выступать сами числа, т.е. значения a[i] ( b[i] ), а в качестве коэффициентов при них — сколько раз это число встречается в массиве ().

Тогда, перемножив эти два многочлена за 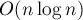O(n log n) , мы получим многочлен 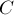, где в качестве степеней будут всевозможные числа вида a[i]+b[j] , а коэффициенты при них будут как раз искомыми количествами

Всевозможные скалярные произведения

Даны два массива a[] и b[] одной длины . Требуется вывести значения каждого скалярного произведения вектора на очередной циклический сдвиг вектора .

Инвертируем массив и припишем к нему в конец нулей, а к массиву — просто припишем самого себя. Затем перемножим их как многочлены. Теперь рассмотрим коэффициенты произведения c[n ldots 2n-1] (как всегда, все индексы в 0-индексации). Имеем:

$c[k] = sum_{i+j=k} a[i] b[j].$

Поскольку все элементы a[i]=0, i=n ldots 2n-1 , то мы получаем:

$c[k] = sum_{i=0}^{n-1} a[i] b[k-i].$

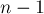Нетрудно увидеть в этой сумме, что это именно скалярное произведение вектора на k-n-1 -ый циклический сдвиг. Таким образом, эти коэффициенты (начиная с n-1 -го и закачивая 2n-2 -ым) — и есть ответ на задачу.

Решение получилось с асимптотикой 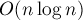O (n log n) .

Две полоски

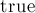Даны две полоски, заданные как два булевских (т.е. числовых со значениями 0 или 1) массива a[] и b[] . Требуется найти все такие позиции на первой полоске, что если приложить, начиная с этой позиции, вторую полоску, ни в каком месте не получится rm true сразу на обеих полосках. Эту задачу можно переформулировать таким образом: дана карта полоски, в виде 0/1 — можно вставать в эту клетку или нет, и дана некоторая фигурка в виде шаблона (в виде массива, в котором 0 — нет клетки, 1 — есть), требуется найти все позиции в полоске, к которым можно приложить фигурку.

Эта задача фактически ничем не отличается от предыдущей задачи — задачи о скалярном произведении. Действительно, скалярное произведение двух 0/1 массивов — это количество элементов, в которых одновременно оказались единицы. Наша задача в том, чтобы найти все циклические сдвиги второй полоски так, чтобы не нашлось ни одного элемента, в котором бы в обеих полосках оказались единицы. Т.е. мы должны найти все циклические сдвиги второго массива, при которых скалярное произведение равно нулю.

Таким образом, эту задачу мы решили за 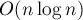O(n log n) .

Источник: http://e-maxx.ru/algo/fft_multiply

Algorithms

The FFT functions (fft, fft2, fftn, ifft, ifft2, ifftn)are based on a library called FFTW [1] [2].

Источник: http://mathworks.com/help/matlab/ref/fft.html

Код

Поэтому код в OP неверен, и вместо этого, по-видимому, необходимо выводить как амплитуду, так и мощность, поскольку нет общего коэффициента нормализации, который мог бы вместить сложные и реальные случаи с четным или нечетным числом временных точек. Суть вы можете найти здесь .

Jonathan H 03 февраля 2016 в 18:43

Я нашел этот онлайн-пример fft ( https://habr.com/post/112068/ ) довольно полезным. Проверьте это:

%% ParametersTm=5;% Length of signal (s)Fd=512;% Sampling frequency (Hz)Ak=0.5;% Constant component (Unit)A1=1;% The amplitude of the first sinusoid (Unit)A2=0.7;% Amplitude of the second sinusoid (Unit)F1=13;% Frequency of the first sinusoid (Hz)F2=42;% Frequency of the second sinusoid (Hz)Phi1=0;% Initial phase of the first sinusoid (Degrees)Phi2=37;% The initial phase of the second sinusoid (Degrees)An=3*A1;% Noise Dispersion (Unit)FftL=1024;% Number of Fourier Spectrum Lines%% Generating work arraysT=0:1/Fd:Tm;% Time ArraysNoise=An*randn(1,length(T));% An array of random noise with a length equal to the array of timeSignal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% Signal array (a mixture of 2x sinusoids and a constant component)%% Spectral representation of the signalFftS=abs(fft(Signal,FftL));% The amplitudes of the Fourier transform of the signalFftS=2*FftS./FftL;% Spectrum normalization by amplitudeFftS(1)=FftS(1)/2;% The normalization of the constant component in the spectrumFftSh=abs(fft(Signal+Noise,FftL));% The amplitudes of the Fourier transform of the signal + noise mixtureFftSh=2*FftSh./FftL;% Spectrum normalization by amplitudeFftSh(1)=FftSh(1)/2;% The normalization of the constant component in the spectrum%% Plottingsubplot(2,1,1);plot(T,Signal);title(‘Signal’);xlabel(‘Time (s)’);ylabel(‘Amplitude (Unit)’);subplot(2,1,2);plot(T,Signal+Noise);title(‘Signal+Noise’);xlabel(‘Time (s)’);ylabel(‘Amplitude (Unit)’);F=0:Fd/FftL:Fd/2-1/FftL;% The frequency array of the calculated Fourier spectrumfigure();subplot(2,1,1);plot(F,FftS(1:length(F)));% Plotting of the spectrum of the Fourier signaltitle(‘Signal spectrum’);xlabel(‘Frequency (Hz)’);ylabel(‘Amplitude (Unit)’);subplot(2,1,2);plot(F,FftSh(1:length(F)));% Plotting of the Fourier signal spectrumtitle(‘Signal spectrum’);xlabel(‘Frequency (Hz)’);ylabel(‘Amplitude (Unit)’);

ARTE 27 декабря 2018 в 17:30

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

Contact your local office

Источник: http://mathworks.com/help/matlab/ref/fft.html