Интеграл от степенной функции

Дифференцирование и интегрирование степенной функции, экспоненты и логарифма – формулы. Выражение интегралов через гипергеометрические функции. Значения некоторых определенных интегралов.

Формула

$$int x^{n} d x=frac{x^{n+1}}{n+1}+C, n neq-1$$

Интеграл от степенной функции равен этой же функции в степени на единицу больше, деленной на эту же степень, плюс постоянная интегрирования.

Заметим, что если $x$ в некоторой степени находится в знаменателе, то применяют свойство $frac{1}{x^{n}}=x^{-n}$ и далее интегрируют по указанной формуле.

Источник: http://webmath.ru/poleznoe/formules_11_2.php

Примеры решения задач

ПРИМЕР 2

Задание

Найти неопределенный интеграл

$[ int{frac{dx}{sqrt[3]{{{x}^{2}}}}} ]$

Решение

Запишем подынтегральную функцию в виде степенной функции по формулам:

$[sqrt[m]{{{x}^{n}}}={{x}^{^{frac{n}{m}}}}]$

$[frac{1}{{{x}^{n}}}={{x}^{-n}}]$

Будем иметь:

$[int{frac{dx}{sqrt[3]{{{x}^{2}}}}}=int{frac{dx}{{{x}^{frac{2}{3}}}}}=int{{{x}^{^{-frac{2}{3}}}}dx}=frac{{{x}^{^{-frac{2}{3}+1}}}}{-frac{2}{3}+1}+C=frac{{{x}^{^{frac{1}{3}}}}}{frac{1}{3}}+C=3sqrt[3]{x}+C]$

Ответ

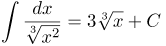Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/integraly/integral-stepennoj-funkcii/

Главные интегралы, которые должен знать каждый студент

Перечисленные интегралы — это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.

Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!

Интеграл от константы

∫ Adx=Ax+C

(1)

Интегрирование степенной функции

В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.

∫ xdx= x 2 2 +C

(2)

∫ x 2 dx= x 3 3 +C

(3)

∫ 1 x dx=2 x +C

(4)

∫ 1 x dx=ln| x |+C

(5)

∫ 1 x 2 dx=− 1 x +C

(6)

∫ x n dx= x n+1 n+1 +C(n≠−1)

(7)

Интегралы от показательной функции и от гиперболических функций

Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.

∫ e x dx= e x +C

(8)

∫ a x dx= a x lna +C(a>0,a≠1)

(9)

∫ shx dx=chx+C

(10)

∫ chx dx=shx+C

(11)

Базовые интегралы от тригонометрических функций

Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен «минус косинусу», а вот интеграл от cosx равен «просто синусу»:

∫ sinxdx=−cosx+C

(12)

∫ cosxdx=sinx+C

(13)

∫ 1 cos 2 x dx=tgx+C

(14)

∫ 1 sin 2 x dx=−ctgx+C

(15)

Интегралы, сводящиеся к обратным тригонометрическим функциям

Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) — частный случай (19).

∫ 1 1+ x 2 dx=arctgx+C=−arcctgx+C

(16)

∫ 1 x 2 + a 2 = 1 a arctg x a +C(a≠0)

(17)

∫ 1 1− x 2 dx=arcsinx+C=−arccosx+C

(18)

∫ 1 a 2 − x 2 dx=arcsin x a +C=−arccos x a +C(a>0)

(19)

Источник: http://repetitor2000.ru/integrals.html

ВВЕДЕНИЕ

Методические указания по выполнению контрольныхработ составлены для студентов всех специальностей Института интегрированных формобучения (ИИФО), занимающихся по ускоренной программе (на базе техникума).

Задания контрольных работ № 3–4 включаютосновные разделы курса «Высшей математики»: неопределенный и определенный интегралы,вычисление площади плоской фигуры, однородные и неоднородные дифференциальные уравнениявторого порядка с постоянными коэффициентами, числовые и степенные ряды, приложениястепенных рядов. Студенту предлагается выполнить 12 заданий (8 – в контрольной работе№ 3; 4 – в контрольной работе № 4) и ответить на теоретические вопросы.

Каждое задание сопровождается решением подобногопримера, что позволит студенту самостоятельно выполнить индивидуальное задание.

Источник: http://vunivere.ru/work78226

Формула интеграла от многочлена

Представим, для справок, формулу интеграла от многочлена в общем виде. Пусть задан многочлен от переменной x степени n
,
где a0, a1, a2, … , an – постоянные, не зависящие от x коэффициенты.

Неопределенный интеграл от многочлена определяется по формуле

,
где C – постоянная интегрирования.

Источник: http://1cov-edu.ru/mat_analiz/integrali/neopredelennie/osnovnye_formuly_integrirovaniya/mnogochleny/

РАЗДЕЛ 1. Неопределенный интеграл

Рассмотрим правила интегрирования неопределенныхпростейших интегралов. Кратко смысл задания сводится к следующему.

При помощи преобразований привести интегралк табличному, затем, используя таблицу интегралов, найти первообразную:

∫f( x )dx = F( x )+C, где f ( x ) – подынтегральнаяфункция; F(x ) – первообразная; C – произвольная постоянная.

Таблица основных интегралов дана ниже, где«a» и «b» – постоянные коэффициенты, причем a ≠ 0, а «b» – любое.

Источник: http://vunivere.ru/work78226

Примеры решений сложных интегралов

Пример 1

Задача

Вычислить интеграл:

$[int frac{dx}{xsqrt{x^{2} - a^{2}}}]$

при помощи подстановки $x = frac{a}{t}$

Решение

Найдём dx:

$dx = -frac{a}{t^{2}}dt$

Преобразуем подынтегральную функцию c учётом подстановки $x = frac{a}{t}$ :

$frac{1}{xsqrt{x^{2} - a^{2}}} = frac{1}{frac{a}{t}sqrt{frac{a^{2}}{t^{2}} - a^{2}}} = frac{t^{2}}{a^{2}sqrt{1 - t^{2}}}$

Искомый интеграл преобразуется к следующему виду:

$[int frac{t^{2}}{a^{2}sqrt{1 - t^{2}}}(-frac{a}{t^{2}}dt) = -frac{1}{a}int frac{dt}{sqrt{1 - t^{2}}} = -frac{1}{a}arcsin{t} + C]$

Перейдём к переменной , для этого из подстановки $x = frac{a}{t}$ выразим через :

$t = frac{a}{x}$

В итоге получим:

$-frac{1}{a}arcsin{frac{a}{x}} + C$

Преобразуем полученный результат с учётом, что $frac{pi}{2} - arcsin{alpha} = arccos{alpha}$

Считая, что $C = frac{1}{a}frac{pi}{2} + C_{1}$ , получим

$-frac{1}{a}arcsin{frac{a}{x}} + C = frac{1}{a}frac{pi}{2} - frac{1}{a}arcsin{frac{a}{x}} + C_{1} = frac{1}{a}(frac{pi}{2} - arcsin{frac{a}{x}}) + C_{1}$

Индекс $C_{1}$ можно обозначить через

Окончательно, получим:

$frac{1}{a}(frac{pi}{2} - arcsin{frac{a}{x}}) + C_{1} = frac{1}{a}arccos{frac{a}{x}} + C$

Ответ

$[int frac{dx}{xsqrt{x^{2} - a^{2}}} = frac{1}{a}arccos{frac{a}{x}} + C]$

Пример 2

Задача

Вычислить интеграл:

$[int frac{dx}{{sqrt{2ax - x^{2}}}}]$

при помощи подстановки x = a(1 - t)

Решение

Найдём dx:

dx = -adt

Преобразуем подынтегральную функцию c учётом подстановки x = a(1 - t) :

$sqrt{2ax - x^{2}} = sqrt{2acdot a(1 - t) - a^{2}{(1 - t)}^{2}} = sqrt{a^{2}{(1 - t)}^{2}} = |a|{(1 - t)}^{2}$

Искомый интеграл преобразуется к следующему виду:

$[int frac{-adt}{|a|sqrt{1 - t^{2}}} = -frac{a}{|a|}int frac{dt}{sqrt{1 - t^{2}}} = frac{a}{|a|}arccos{t} + C = pmarccos{t} + C]$

Перейдём к переменной , для этого из подстановки x = a(1 - t) выразим через :

$t = 1 - frac{x}{a} = frac{a - x}{a}$

В итоге получим:

$[int frac{-adt}{|a|sqrt{1 - t^{2}}} = pmarccos{frac{a - x}{a}} + C]$

Ответ

$[int frac{dx}{{sqrt{2ax - x^{2}}}} = pmarccos{frac{a - x}{a}} + C]$

Пример 3

Задача

Вычислить интеграл от дроби:

$[int frac{dx}{2x -1}]$

Решение

$[int frac{dx}{2x -1} = frac{1}{2}intfrac{2dx}{2x - 1} = frac{1}{2}ln|2x - 1| + C]$

Ответ

$[int frac{dx}{2x -1} = frac{1}{2}ln|2x - 1| + C]$

Пример 4

Задача

Вычислить интеграл:

$[int sqrt{2ax - x^{2}}dx]$

при помощи тригонометрической подстановки x = asin{t}

Решение

Найдём dx:

dx = acos{t}dt

Преобразуем подынтегральную функцию c учётом подстановки x = asin{t} :

$sqrt{a^{2} - x^{2}} = sqrt{a^{2} - a^{2}sin^{2}{t}} = sqrt{a^{2}(1 - sin^{2}{t})} = sqrt{a^{2}cos^{2}{t}} = acos{t}$

Искомый интеграл преобразуется к следующему виду:

$[int acos{t}(acos{t}dt) = a^{2}int cos^{2}{t}dt]$

Интеграл вида относится к табличным и равен:

$[int cos^{2}{t}dt = frac{1}{2}(t + sin{t}cos{t}) + C]$

Поэтому:

$[a^{2}int cos^{2}{t}dt = a^{2}frac{1}{2}(t + sin{t}cos{t}) + C]$

Перейдём к переменной , для этого из подстановки x = asin{t} выразим t, sin{t}, cos{t} через :

$t = arcsin{frac{x}{a}}, sin{t} = frac{x}{a}, cos{t} = sqrt{1 - sin^{2}{t}} = sqrt{1 - frac{x^{2}}{a^{2}}} = frac{sqrt{a^{2} - x^{2}}}{a}$

В итоге получим:

$[a^{2}frac{1}{2}(t + sin{t}cos{t}) + C = a^{2}frac{1}{2}(arcsinfrac{x}{a} + frac{x}{a}frac{sqrt{a^{2} - x^{2}}}{a}) + C]$

$[a^{2}frac{1}{2}(t + sin{t}cos{t}) + C = frac{x}{2}sqrt{a^{2} - x^{2}} + frac{a^{2}}{2}arcsin{frac{x}{a}} + C]$

Ответ

$[int sqrt{2ax - x^{2}}dx = frac{x}{2}sqrt{a^{2} - x^{2}} + frac{a^{2}}{2}arcsin{frac{x}{a}} + C]$

Пример 5

Задача

Вычислить интеграл:

$[int frac{x^{2}}{sqrt{a^{2} - x^{2}}}dx]$

при помощи тригонометрической подстановки x = asin{t}

Решение

Найдём dx:

dx = acos{t}dt

Преобразуем подынтегральную функцию c учётом подстановки x = asin{t} :

$frac{x^{2}}{sqrt{a^{2} - x^{2}}} = frac{a^{2}sin^{2}t}{sqrt{a^{2} - a^{2}sin^{2}{t}}} = frac{a^{2}sin^{2}t}{sqrt{a^{2}(1 - sin^{2}{t})}} = frac{a^{2}sin^{2}t}{sqrt{a^{2}cos^{2}{t}}} = frac{a^{2}sin^{2}t}{acos{t}}$

Искомый интеграл преобразуется к следующему виду:

$[int frac{a^{2}sin^{2}t}{acos{t}}acos{t}dt = a^{2}int sin^{2}{t}dt]$

Интеграл вида относится к табличным и равен:

$[int sin^{2}{t}dt = frac{1}{2}(t - sin{t}cos{t}) + C]$

Поэтому:

$[a^{2}int sin^{2}{t}dt = a^{2}frac{1}{2}(t - sin{t}cos{t}) + C]$

Перейдём к переменной , для этого из подстановки x = asin{t} выразим t, sin{t}, cos{t} через :

$t = arcsin{frac{x}{a}}, sin{t} = frac{x}{a}, cos{t} = sqrt{1 - sin^{2}{t}} = sqrt{1 - frac{x^{2}}{a^{2}}} = frac{sqrt{a^{2} - x^{2}}}{a}$

В итоге получим:

$[a^{2}frac{1}{2}(t - sin{t}cos{t}) + C = frac{a^{2}}{2}(arcsinfrac{x}{a} - frac{x}{a}frac{sqrt{a^{2} - x^{2}}}{a}) + C]$

$[a^{2}frac{1}{2}(t - sin{t}cos{t}) + C = frac{a^{2}}{2}arcsinfrac{x}{a} - frac{x}{2}sqrt{a^{2} - x^{2}} + C]$

Ответ

$[int frac{x^{2}}{sqrt{2ax - x^{2}}}dx = frac{a^{2}}{2}arcsinfrac{x}{a} - frac{x}{2}sqrt{a^{2} - x^{2}} + C]$

Пример 6

Задача

Вычислить интеграл:

$[int sqrt{frac{1 - x}{1 + x}}dx]$

при помощи подстановки x = sin{t}

Решение

Найдём dx:

dx = cos{t}dt

Преобразуем подынтегральную функцию c учётом подстановки x = sin{t} :

$sqrt{frac{1 - x}{1 + x}} = sqrt{frac{1 - sin{t}}{1 + sin{t}}} = sqrt{frac{{(1 - sin{t})}^{2}}{(1 + sin{t})(1 - sin{t})}} = frac{sqrt{{(1 - sin{t})}^2}}{sqrt{1 - sin^2{t}}} = frac{1 - sin{t}}{cos{t}}$

Искомый интеграл преобразуется к следующему виду:

$[int sqrt{frac{1 - x}{1 + x}}dx = int frac{1 - sin{t}}{cos{t}}cos{t}dt = int (1 - sin{t})dt]$

$[int sqrt{frac{1 - x}{1 + x}}dx = t + cos{t} + C]$

Перейдём к переменной , для этого из подстановки x = sin{t} выразим через :

t = arcsin{x}

В итоге получим:

t + cos{t} + C = arcsin{x} + cos{(arcsin{x})} + C

Т.к. $cos{(arcsin{x})} = sqrt{1 - x^{2}}$ , то

$arcsin{x} + cos{(arcsin{x})} + C = arcsin{x} + sqrt{1 - x^{2}} + C$

Ответ

$[int sqrt{frac{1 - x}{1 + x}}dx = arcsin{x} + sqrt{1 - x^{2}} + C]$

Пример 7

Задача

Вычислить интеграл:

$[int frac{dx}{sqrt{1 + x^{2}}}]$

при помощи подстановки x = ctg{t}

Решение

Найдём dx:

$dx = -frac{1}{sin^2{t}}dt$

Преобразуем подынтегральную функцию c учётом подстановки x = ctg{t} :

$sqrt{1 + x^{2}} = sqrt{1 + ctg^{2}{t}} = sqrt{1 + frac{cos^{2}{t}}{sin^{2}{t}}} = sqrt{frac{sin^{2}{t} + cos^{2}{t}}{sin^{2}{t}}}$ = $frac{1}{sin{t}}$

Искомый интеграл преобразуется к следующему виду:

$[int frac{dx}{sqrt{1 + x^{2}}} = -int frac{dt}{sin{t}} = -ln tg{frac{t}{2}} + C]$

$-ln tg{frac{t}{2}} + C = ln {left(tg{frac{t}{2}}right)}^{-1} + C$

$-ln tg{frac{t}{2}} + C = ln {ctg{frac{t}{2}}} + C$

$ctg{frac{t}{2}} = frac{cos{frac{t}{2}}}{sin{frac{t}{2}}} = frac{2cos^{2}{frac{t}{2}}}{2sin{frac{t}{2}}cos{frac{t}{2}}} = frac{1 - cos{t}}{sin{t}}$ = $frac{1}{sin{t}} + ctg{t}$

Перейдём к от к переменной :

$frac{1}{sin{t}} = sqrt{1 + x^{2}}, ctg{t} = x$

$ln {ctg{frac{t}{2}}} + C = ln (frac{1}{sin{t}} + ctg{t}) + C = ln(x + sqrt{1 + x^{2}}) + C$

Ответ

$[int frac{dx}{sqrt{1 + x^{2}}} = ln(x + sqrt{1 + x^{2}}) + C]$

Пример 8

Задача

Вычислить интеграл:

$[int frac{dx}{xsqrt{x^{2} - a^{2}}}]$

при помощи подстановки $z = sqrt{x^{2} - a^{2}}$

Решение

Выразим подынтегральную функцию через переменную :

$x^{2} - a^{2} = z^{2}, x^{2} = a^{2} + z^{2}, 2xdx = 2zdz, xdx = zdz$

Разделим обе части равенства xdx = zdz на $x^{2}$ :

$frac{xdx}{x^{2}} = frac{zdz}{x^{2}}$

В правой части равенства заменим $a^{2} + z^{2}$ на $x^{2}$ :

$frac{xdx}{x} = frac{zdz}{a^{2} + z^{2}}$

$frac{dx}{xsqrt{x^{2} - a^{2}}} = frac{zdz}{(a^{2} + z^{2})z} = frac{dz}{a^{2} + z^{2}}$

$[intfrac{dz}{a^{2} + z^{2}} = frac{1}{a} arctgfrac{z}{a} + C]$

Переходя к переменной , получаем:

$frac{1}{a} arctgfrac{z}{a} + C = frac{1}{a} arctgfrac{sqrt{x^{2} - a^{2}}}{a} + C$

Ответ

$int frac{dx}{xsqrt{x^{2} - a^{2}}} = frac{1}{a} arctgfrac{sqrt{x^{2} - a^{2}}}{a} + C$

Пример 9

Задача

Вычислить интеграл:

$[int frac{dx}{sqrt{x + 2} + 3}]$

при помощи подстановки t = sqrt{x + 2}

Решение

Выразим подынтегральную функцию через переменную :

$x + 2 = t^{2}, x = t^{2} - 2, dx = 2tdt$

$frac{dx}{sqrt{x + 2} + 3} = frac{2tdt}{t + 3}$

$[intfrac{2tdt}{t + 3} = 2intfrac{t + 3 - 3}{t + 3}dt]$

$[2intfrac{t + 3 - 3}{t + 3}dt = 2intleft(1 - frac{t}{t + 3}right)dt]$

$[2intleft(1 - frac{t}{t + 3}right)dt = 2[t - 3ln(t + 3)] + C]$

Переходя к переменной , и учитывая, что t = sqrt{x + 2} получаем:

2[t - 3ln(t + 3)] + C = 2[sqrt{x + 2} - 3ln||sqrt{x + 2} + 3] + C

Ответ

$[int frac{dx}{sqrt{x + 2} + 3} = 2[sqrt{x + 2} - 3ln||sqrt{x + 2} + 3] + C]$

Пример 10

Задача

Вычислить интеграл:

$[int frac{dx}{sqrt{a^{2} - x^{2}}}]$

при помощи подстановки $t(a - x) = sqrt{a^{2} - x^{2}}$

Решение

Выразим подынтегральную функцию через переменную :

$a^{2} - x^{2} = t^{2}{(a - x)}^{2}, a + x = t^{2}(a - x)$

$x = afrac{t^{2} - 1}{t^{2} + 1}, dx = frac{4atdt}{{(t^{2} + 1)}^{2}}$

$sqrt{a^{2} - x^{2}} = frac{2at}{t^{2} + 1}$

$[2intfrac{frac{4atdt}{{(t^{2} + 1)}^{2}}}{frac{2at}{t^{2} + 1}} = intfrac{2dt}{t^{2} + 1}]$

$[intfrac{2dt}{t^{2} + 1} = 2 arctg{t} + C]$

Переходя к переменной , и учитывая, что $t = frac{sqrt{a^{2} - x^{2}}}{a - x}$ получаем:

$2 arctg{t} + C = 2 arctg{frac{sqrt{a^{2} - x^{2}}}{a - x}} + C = 2 arctg{sqrt{frac{a + x}{a - x}}} + C$

Ответ

$[int frac{dx}{sqrt{a^{2} - x^{2}}} = 2 arctg{sqrt{frac{a + x}{a - x}}} + C]$

Примеры решения сложных интегралов с ответами обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Источник: http://nauchniestati.ru/spravka/primery-resheniya-slozhnyh-integralov-s-otvetami/