Квадратичная функция. Парабола

Как построить график квадратичной функции Параболы. Рассмотрим алгоритм построения на примерах разных видов уравнений.

Алгоритм построения графика параболы

Если парабола задана уравнением $y=ax^{2} +bx+c$ , то чтобы построить ее график, понадобится:

Выяснить направление ветвей параболы: если коэффициент 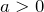, то ветви направлены вверх, а если 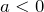– вниз.
Определить координаты вершины параболы. Чтобы определить абсциссу вершины параболы пользуются формулой
$[x_{bep} =-frac{b}{2a} ]$

Для определения ординаты вершины параболы нужно подставить в уравнение параболы вместо 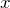найденное в предыдущем шаге значение $x_{bep}$ :

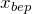$[y_{bep} =yleft(x_{bep} right)=acdot x_{bep}^{2} +bcdot x_{bep} +c]$
Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси .
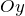Найти точки пересечения с осями координат:

– с осью – найти корни уравнения $ax^{2} +bx+c=0$ , если уравнение не имеет действительных корней, то график не пересекает ось абсцисс,

– с осью 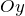– подставить в уравнение значение

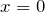и вычислить значение

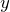Найти координаты произвольной точки 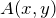A(x,y) , которая принадлежит параболе. Для этого возьмем произвольное значение 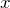и подставим его в уравнение параболы. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси.

Источник: http://ru.solverbook.com/spravochnik/formuly-po-geometrii/parabola/postroenie-paraboly/

Что называют квадратичной функцией

Запомните! $!$

Квадратичная функция — это функция вида

y = ax2 + bx + c,

где

— заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит «x» — это «2», то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».

Квадратичная функция	Коэффициенты
y = 2×2 − 7x + 9	a = 2 b = −7 с = 9
y = 3×2 − 1	a = 3 b = 0 с = −1
y = −3×2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните! $!$

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

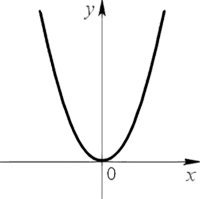
$парабола - график квадратичной функции$

Также парабола может быть перевернутой.

$перевернутая парабола$

Существует четкий алгоритм действий при построении графика квадратичной функции.Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x2 −7x + 10».

Направление ветвей параболы
Запомните! $!$
Если «a > 0», то ветви направлены вверх. $парабола маленькая$

Если «a », то ветви направлены вниз. $перевернутая парабола маленькая$

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх. $перевернутая парабола мальнькая$
Координаты вершины параболы
Запомните! $!$
Чтобы найти «x0» (координата вершины по оси «Ox») нужно использовать формулу:

Найдем «x0» для нашей функции «y = x2 −7x + 10».

Теперь нам нужно найти «y0» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x0» в исходную функцию.Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».

y0(3,5) = (3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 = −12,25 + 10 = −2,25

Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».

$вершина параболы$

Нули функции

Для начала давайте разберемся, что называют нулями функции.

Запомните! $!$

Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).

Наглядно нули функции на графике выглядят так:

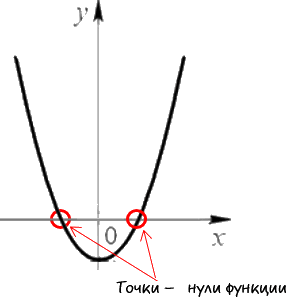
$нули функции$

Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Запомните! $!$

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».

Подставим в заданную функцию «y = x2 −7x + 10» вместо «y = 0» и решим полученное квадратное уравнение относительно «x» .

0 = x

−7x + 10

−7x + 10 = 0

1;2

7 ± √49 − 4 · 1 · 10

2 · 1

1;2

x1 =	x2 =
x1 =	x2 =
x1 = 5	x2 = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox». Назовем эти точки и выпишем их координаты.

(·) B (5; 0)
(·) C (2; 0)

Отметим полученные точки («нули функции») на системе координат.

$отмечаем нули функции на системе координат$

Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к осисимметрии. Числа запишем в таблицу в порядке возрастания.

Для каждого выбранного значения «x» рассчитаем «y».
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 = 4
- y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 = −2
- y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 = −2
- y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 = 4
Запишем полученные результаты в таблицу.

Отметим полученные точки графика на системе координат (зеленые точки).

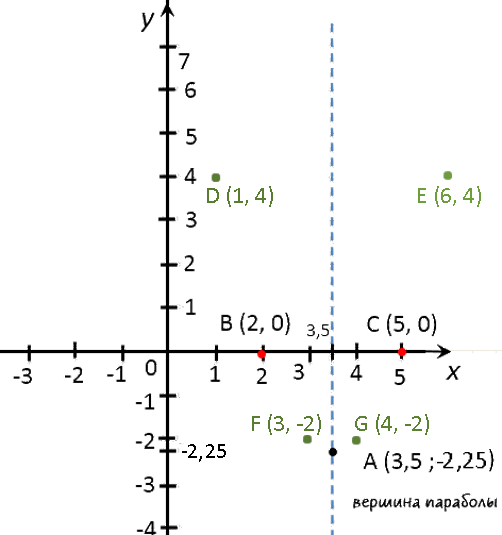
$дополнительные точки для построения$

Теперь мы готовы построить график.На забудьте после построения подписать график функции.

$график параболы$

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.Только теперь запишем алгоритм построения коротко без подробностей.

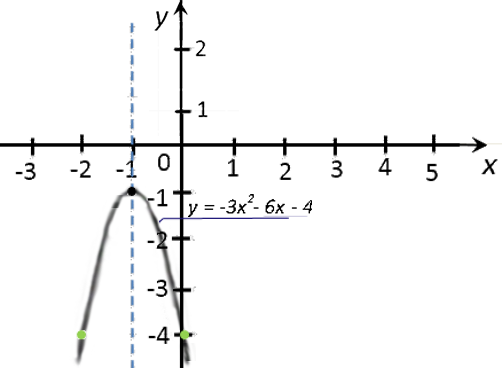
Пусть требуется построить график функции «y = −3×2 − 6x − 4».

Направление ветвей параболы «

a = −3» — ветви параболы направлены вниз. $перевернутая парабола маленькая$ Координаты вершины параболы

x0 =
x0 = = = −1

y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.

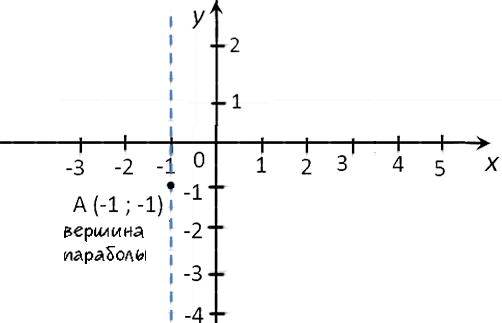$вершина параболы -3x^2 - 6x - 4$ Нули функции

Точки пересечения с осью «Ox» (y = 0).

0 = −3×2 − 6x − 4

−3×2 − 6x − 4 = 0 |·(−1)

3×2 + 6x + 4 = 0

x1;2 =

−6 ± √62 − 4 · 3 · 4

2 · 1

x1;2 =
x1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось «Ox».

Вспомогательные точки для: «x = −3»; «x = −2»; «x = 0»; «x = 1». Подставим в исходную функцию «y = −3×2 − 6x − 4».

y(−3) = −3 · (−3)2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
y(−2) = −3 · (−2)2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
y(0) = −3 · 02 − 6 · 0 − 4 = −4
y(1) = −3 · 12 − 6 · 1 − 4 = −3 −6 − 4 = −13

x	−3	−2	0	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки «(−2; −4)» и «(0; −4)». Построим и подпишем график функции.

$график функции -3x^2 - 6x - 4$

Источник: http://math-prosto.ru/?page=pages/quadratic_function/quadratic_function_how_to_draw_parabola.php

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ: наглядно.

Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Источник: http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola

Выделение полного квадрата

Напомню, что мы можем представить функцию ( y=a{{x}^{2}}+bx+c) в таком виде:

( y=a{{left( x-p right)}^{2}}+q).

Например: ( y={{x}^{2}}-6x+5={{left( x-3 right)}^{2}}-4).

Или: ( 2{{x}^{2}}+6x+1=2{{left( x+1,5 right)}^{2}}-3,5).

Что это нам дает?

Дело в том, что число, которое вычитается из ( displaystyle x) в скобках (( displaystyle p)) – это абсцисса вершины параболы, а слагаемое за скобками (( displaystyle q)) – ордината вершины.

Это значит, что, построив параболу ( y=a{{x}^{2}}), нужно будет просто сместить ось ( displaystyle Oy) на ( displaystyle p) влево и ось ( displaystyle Ox) на ( q) вниз.

Пример: построим график функции ( y=0,5{{x}^{2}}+2x+1).

Выделим полный квадрат:

( y=0,5left( {{x}^{2}}+4x right)+1=0,5left( {{x}^{2}}+4x+4-4 right)+1=0,5left( {{x}^{2}}+4x+4 right)-2+1=0,5{{left( x+2 right)}^{2}}-1)

Какое число вычитается из ( displaystyle x) в скобках? Это ( displaystyle -2) (а не ( displaystyle 2), как можно решить, не подумав).

Итак, строим параболу ( y=0,5{{x}^{2}}):

Теперь смещаем ось ( displaystyle Ox) на ( displaystyle -1) вниз, то есть на ( displaystyle 1) вверх:

А теперь – ( displaystyle Oy) на ( displaystyle -2) влево, то есть на ( displaystyle 2) вправо:

Вот и все. Это то же самое, как переместить параболу ( y=0,5{{x}^{2}}) вершиной из начала координат в точку ( displaystyle (-2;-1)), только прямые оси двигать намного легче, чем кривую параболу.

Теперь, как обычно, сам.

Источник: http://youclever.org/book/postroenie-grafika-kvadratichnoj-funktsii-1/

Тема: «Кривые второго порядка. Парабола»

Цель: формирование умений составлять уравнения параболы, исследовать форму и расположение параболы;

формирование общих компетенций, включающими в себя способность:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.

Методические указания и теоретические сведения к практической работе

Парабола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

Каноническое уравнение параболы в прямоугольной системе координат:

(или , если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.

Парабола, заданная квадратичной функцией

Квадратичная функция при также является уравнением параболы и графически изображается той же параболой, что и но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

где — дискриминант квадратного трёхчлена.

Общее уравнение параболы

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант равен нулю.

Пример 1. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением .

Решение. Из данного канонического уравнения параболы следует, что , т.е. ,откуда .Значит, точка — фокус параболы, а — уравнение ее директрисы.

Пример 2. Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты .

Решение. Согласно условию, фокус параболы расположен на отрицательной полуоси , т.е. ее уравнение имеет вид: x2= — 2py

Так как , то , откуда .Итак, уравнение параболы есть , а уравнение ее директрисы .

Пример 3. Составить уравнение параболы, имеющей вершину в начале координат, симметричной оси Ох и проходящей через точку .

Решение. Из условия заключаем, что уравнение параболы следует искать в виде .

Так как точка принадлежит параболе , то ее координаты удовлетворяют этому уравнению: 36= — 2р*(-3); 2р=12.

Итак, уравнение параболы имеет вид .

Пример 4. Парабола симметрична относительно оси Ox, проходит через точку

A(4, -1), а вершина ее лежит в начале координат. Составить ее уравнение.

Решение.Так как парабола проходит через точку A(4, -1) с положительной абсциссой, а ее осью служит ось Ox, то уравнение параболы следует искать в виде y2 = 2px. Подставляя в это уравнение координаты точки A, будем иметь

искомым уравнением будет

Эскиз этой параболы показан на рисунке

Пример 5.Парабола y2 = 2px проходит через точку A(2, 4). Определить ее параметр p.

Решение. Подставляем в уравнение параболы вместо текущих координат координаты точки A (2, 4). Получаем

42 = 2p*2; 16 = 4p; p = 4.

Пример 6. Привести к каноническому (простейшему) виду уравнение параболы

y = 2x2 + 4x + 5 и найти координаты ее вершины.

Решение. Уравнение y = 2x2 + 4x + 5 преобразуем, выделив в правой части полный квадрат:

y = 2(x2 + 2x) + 5,

y = 2[(x + 1)2 — 1] + 5,

y = 2(x + 1)2 + 3,

y — 3 = 2(x + 1)2;

пусть теперь x1 = x + 1, y1 = y — 3. Из сравнения с формулами

координаты нового начала: x0 = -1; y0 = 3. Уравнение параболы примет вид

Эскиз параболы показан на рисунке.

Пример 7.Упростить уравнение параболы y = x2 — 7x + 12, найти координаты ее вершины и начертить эскиз кривой.

Решение. Выделим в правой части уравнения y = x2 — 7x + 12 полный квадрат по способу, указанному выше в задаче, и получим

или

Положим

Отсюда из сравнения с формулами

координаты нового начала, т. е. вершины параболы, будут . После переноса начала координат в точку уравнение параболы примет наиболее простой вид . Эскиз кривой представлен на рисунке.

Пример 8. Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой и окружности и симметрична относительно оси .

Решение. Найдем точки пересечения заданных линий, решив совместно их уравнения:

В результате получим два решения и . Точки пересечения и . Так как парабола проходит через точку и симметрична относительно оси , то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид . Так как парабола проходит через точку , то координаты этой точки удовлетворяют уравнению параболы: , ,

Итак, уравнением параболы будет , уравнение директрисы или , откуда

Ответ. ;

Пример 9. Мостовая арка имеет форму параболы. Определить параметр этой параболы, зная, что пролет арки равен , а высота

Решение.Выберем прямоугольную систему координат так, чтобы вершина параболы (мостовой арки) находилась в начале координат, а ось симметрии совпадала с отрицательным направлением оси . В таком случае каноническое уравнение параболы имеет вид , а концы хорды арки и . Подставив координаты одного из концов хорды (например, ) в уравнение параболы и решив полученное уравнение относительно , получим

Ответ.

Задание 1.

а) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у2=16р.

б) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

у2= —18р.

Задание 2.

а) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; -7).

б) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; 4).

Задание 3.

а) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (-2; — 4). Начертить эскиз данной кривой.

б) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (3; — 5). Начертить эскиз данной кривой.

Задание 4.

а) Парабола y2 = 2px проходит через точку A(4; 8). Определить ее параметр p.

б) Парабола y2 = —2px проходит через точку A(-4; -8). Определить ее параметр p.

Задание 5.

а) Привести к каноническому (простейшему) виду уравнение параболы y = 2x2 + 8x + 5 и найти координаты ее вершины. Начертить эскиз данной кривой.

б) Привести к каноническому (простейшему) виду уравнение параболы y = 4x2 + 16x +10 и найти координаты ее вершины. Начертить эскиз данной кривой.

Задание 6. а) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 2х + 2у=0 и окружности х2+у2 – 4х=0 и симметрична относительно оси Оу.

б) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 3х + 3у=0 и окружности 2х2 + 2у2 — 8х=0 и симметрична относительно оси Ох.

Задание 7. а) Арка здания имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 12 м, а высота 4 м.

б) Арка дома имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 14 м, а высота 6 м.

Отчет о практической работе

Тема практической работы

Цель практической работы
Умения

В ходе выполнения практической работы я научился (закрепил умения) вычислять…

Я получил (совершенствовал) практические навыки…

Знания

- В ходе практической работы я получил новые знания. Узнал, что …

Выводы

Мне было сложно выполнять…, потому, что…

Мне было несложно выполнять…, потому, что…

Источник: http://infourok.ru/prakticheskaya-rabota-po-visshey-matematike-na-temu-parabola-reshenie-zadach-4004542.html

Видеоуроки с параболой.

Графики квадратичной функции и коэффициенты квадратного трёхчлена.

При просмотре видео старайтесь следить одновременно за положением графика и формулой функции в нижней части экрана.

Положение и вид параболы в зависимости от знака и значения коэффициента а — коэффициента при х2.

Положение и вид параболы в зависимости от знака и значения коэффициента b — коэффициента при х.

Положение и вид параболы в зависимости от знака и значения параметра c.

Построение параболы по характерным точкам.

Построение графика квадратичной функции

y = ax2 + bx + c

по характерным точкам. Этот алгоритм позволяет построить параболу с минимальным количеством вычислений и при этом с идеальной точностью для решения экзаменационных задач по математике.

Быстрое построение параболы как графика квадратичной функции.

Другие случаи. Примеры построения.

Задачи на анализ графика квадратичной функции.

Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.

Перейдите на главную страницу.

Источник: http://mathematichka.ru/school/functions/quadratic.html

Как узнать, что перед нами уравнение параболы?

Если определения из учебника кажутся сложными, можно запомнить так:
Парабола – это график КВАДРАТичной функции.
Уравнение квадратичной функции выглядит почти так же, как квадратное уравнение:

Т.е. самая большая степень икса — вторая.

Оно может быть полным или неполным, но всегда содержит Х².

Источник: http://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/parabola-vse-chto-nujno-znat-o-funkcii-5ff12009fe4e686f6a364945

Построение квадратичной функции

Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая.
b — второй коэффициент, который отвечает за смещение параболы от центра координат.
с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x2:

График квадратичной функции

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:

x	-2	-1		1	2
y	4	1		1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.

График функции y = –x2 выглядит, как перевернутая парабола:

График функции y = –x2

Зафиксируем координаты базовых точек в таблице:

x	-2	-1		1	2
y	-4	-1		-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:

Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

условие нахождения точек пересечения оси ОХ

Если a > 0, то график выглядит как-то так:

график при условии a > 0

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции. график со всеми разобранными условиями

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

формула нахождения координат вершины параболы график к формуле нахождения координат вершины параболы

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

основные параметры графика квадратичной функции

Источник: http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola

Квадратичная функция и её коэффициенты

Смотрим на уравнение:
X и Y – координаты точек
А где наш k?.. А его нет, потому что в этом уравнении целых три самостоятельных коэффициента: а, в, с.
а– это старший коэффициент, он стоит перед Х² и может быть любым числом, кроме ноля.
в– это средний коэффициент, он стоит перед Х и может быть любым числом.
с – свободный член, потому что после него вообще нет Х, и он тоже может быть любым числом.
Т.е. а≠0; в и с – любые числа.
(Понимаете? Если а будет равно нулю, то Х² просто исчезнет – парабола уже не получится!)

Источник: http://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/parabola-vse-chto-nujno-znat-o-funkcii-5ff12009fe4e686f6a364945

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/formuly-po-geometrii/parabola/postroenie-paraboly/

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Источник: http://skysmart.ru/articles/mathematic/kvadratichnaya-funkciya-parabola

Построим простые графики:

Чему равны коэффициенты в этих уравнениях?

Ясно, что b и С равны нулю. Но чему равно а?

Чтобы построить графики, нужно найти координаты нескольких точек:
1. Возьмём любыечисла и подставим их вместо Х. Да, в квадрат мы можем возвести абсолютно любое число!
2. Посчитаем Y для каждого Х и запишем их парами.

Вот такие графики у нас получились:

Область определения и область значения

Область определения – это все Х, которые мы можем подставить в уравнение. В квадрат можно возвести любое число: положительное, отрицательное, ноль. Значит, Х – любое число!
Записать нужно так: D (f) = (- ∞; ∞)
(Запоминаем: ОпреДеление – D)

Область значения – это все Y, которые мы можем получить.
Давайте посмотрим на графики и сравним результаты:

Вывод:
Область значения квадратичной функции легко определить по графику.

Возрастание и убывание функции, её минимальное и максимальное значение

Смотрим на графики: Парабола состоит из двух ветвей. Одна из ветвей идёт вниз, а другая вверх. Смотрим всё слева направо!

Интервалы строго возрастания/убывания функции

Ветви вверх:
функция убывает на промежутке (-∞;0) – не возрастает (-∞ ;о];
возрастает на промежутке (0; ∞) – не убывает [0; ∞).
Ветви вниз:
функция возрастает на промежутке (-∞;0) – не убывает (-∞ ;о];
убывает на промежутке (0; ∞) – не возрастает [0; ∞).

Вынуждена добавить замечание. По поводу вхождения 0 в промежутки возрастания и убывания возникла дискуссия на нескольких ресурсах интернета. Своим ученикам я советую придерживаться правила: как быстро решать, вычислять, находить — учимся у репетитора; как правильно оформлять — спрашиваем школьного учителя.

Источник: http://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/parabola-vse-chto-nujno-znat-o-funkcii-5ff12009fe4e686f6a364945

Как найти все коэффициенты и восстановить уравнение функции по графику!

Начинается самое интересное. Возьмём готовый график и восстановим уравнение функции! Т.е. вычислим все коэффициенты.

Прошу прощения: ещё не научилась строить приличные графики…

Начнём со свободного члена С – это самое простое!

С – это точка пересечения графика с осью Y. И всё.
Наша парабола пересекает игрек на отметке – 3 ? Значит, С= -3.

Как найти а?

Чуть «заморочнее», но тоже легко. Есть специальная формула, которую мы сейчас запомним:

Делаем так:

Нашли а! а =1

Осталось найти b!

Мы уже знаем: а=1, с= -3.
Ещё мы выбрали точку (-1;0) и видим координаты вершины (1; -4)
Есть два пути. Выбирайте, какой вам больше понравится:

Нашли b! b = -2

Восстановим уравнение функции и пойдём отдыхать:

Все коэффициенты нашли: а= 1, b = -2; с = -3

Подставляем их сюда: y = ах² + bx+c = 1*x²+ (-2)*x+ (-3)

Получаем: y = х² -2x – 3

На сегодня хватит. Скоро будем разбирать варианты задания 11. Статьи по алгебре будут выходить один раз в сутки и висеть тут – никуда не денутся. А если денутся, в ВК меня найдёте)

Статью о гиперболе можно посмотреть здесь: https://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/giperbola-vse-chto-nujno-znat-k-oge-5fef1a68fe4e686f6a56a05b

А здесь — прямая: https://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/priamaia-y—kx—b-vse-chto-nujno-znat-k-oge-5feb44d1e08bb3522f0f5b4a

Источник: http://zen.yandex.ru/media/id/5fb39ed1f83c9a6f822bd270/parabola-vse-chto-nujno-znat-o-funkcii-5ff12009fe4e686f6a364945