Внесение под знак дифференциала, с примерами

При внесении/подведение под знак дифференциала необходимо применять простейшие преобразования дифференциала и табличные интегралы. Теория и примеры решений

Суть метода

Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если

При внесении под знак дифференциала необходимо иметь в виду простейшие преобразования дифференциала:

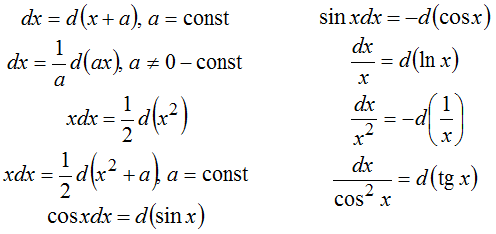
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида

Поэтому имеют место следующие формулы для неопределенных интегралов:

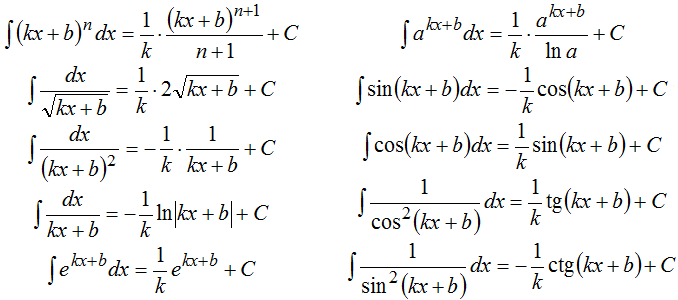
Источник: http://ru.solverbook.com/spravochnik/integraly/vnesenie-pod-znak-differenciala/

Первый способ

Так как $(3x+2)^2=9x^2+12x+4$, то $int (3x+2)^2 dx=int (9x^2+12x+4)dx$. Представляя интеграл $int (9x^2+12x+4)dx$ в виде суммы трёх интегралов и вынося константы за знаки соответствующих интегралов, получим:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx$$

Чтобы найти $int x^2 dx$ подставим $u=x$ и $alpha=2$ в формулу №1 таблицы интегралов: $int x^2 dx=frac{x^{2+1}}{2+1}+C=frac{x^3}{3}+C$. Аналогично, подставляя $u=x$ и $alpha=1$ в ту же формулу из таблицы, будем иметь: $int x^1 dx=frac{x^{1+1}}{1+1}+C=frac{x^2}{2}+C$. Так как $int 1 dx=x+C$, то:

$$9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=9cdotfrac{x^3}{3}+12cdot frac{x^2}{2}+4cdot x+C=3x^3+6x^2+4x+C.$$

Полное решение без пояснений таково:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=\=9cdotfrac{x^3}{3}+12cdot frac{x^2}{2}+4cdot x+C=3x^3+6x^2+4x+C.$$

Источник: http://math1.ru/education/indef_int/intdif.html

Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил:

То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.

Пример 1

Найти неопределенный интеграл. Выполнить проверку.

Смотрим на таблицу интегралов и находим похожую формулу: . Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию  под знак дифференциала:

Раскрывая дифференциал, легко проверить, что:

Фактически  и  – это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: ?  Почему так, а не иначе?

Формула  (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной , но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ ( – в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.

Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл . Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент  и формулой я сразу воспользоваться не могу. Однако если мне удастся получить  и под знаком дифференциала, то всё будет нормально. Если я запишу , тогда . Но в исходном интеграле  множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на ». В ходе примерно таких мысленных рассуждений и рождается запись:

Теперь можно пользоваться табличной формулой :

Готово

Единственное отличие, у нас не буква «икс», а сложное выражение .

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции . По сути дела подведение функции под знак дифференциала и  – это два взаимно обратных правила.

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .

Подводим функцию  под знак дифференциала:

Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: . Ага, получается , значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
Далее используем табличную формулу :

Проверка:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

И так далее.

В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная  входит с единичным коэффициентом, например:

Строго говоря, решение должно выглядеть так:

Как видите, подведение функции  под знак дифференциала прошло «безболезненно»,  без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла  в таблице вообще-то нет.

Источник: http://mathprofi.ru/metod_zameny_peremennoi.html

Таблица первообразных

Источник: http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/metod-podvedenija-pod-znak-differentsiala-pri-inte/

Подведение под знак дифференциала — что это такое?

Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например, , , и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.

Цель подведения под знак дифференциала — получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов. Тогда путём преобразований подынтегрального выражения получим простую функцию переменной и эта переменная будет находится и под знаком дифференциала d.

Решение заключается в том, что аргументом подынтегральной функции становится промежуточный аргумент («внутренняя» функция исходной сложной функции, например, , , и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.

В примерах вместо буквы u будем использовать букву t: так наши решения будут близки к наглядно понятному методу замены переменной. Кстати, в некоторых источниках метод подведения под знак дифференциала считается частным случаем метода замены переменной.

Повторим: наиболее частый случай, когда выгодно применять подведение под знак дифференциала — подынтегральное выражение представляет собой сложную функцию. Но это не единственный случай, когда требуется применять этот метод интегрирования. Другой распространённый случай — когда нет смысла использовать замену переменной, так как это делает вычисления громоздкими. Тогда, чтобы вычисления были короче, можно использовать подведение под знак дифференциала.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Источник: http://function-x.ru/integral103.html

11.1.4. Непосредственное интегрирование

Что такое непосредственное интегрирование? Это интегрирование с использованием свойств и простейшей таблицы интегралов (Интегралы). Рассмотренный метод подведения под знак дифференциала (занятие 11.1.

3) также относится к непосредственному интегрированию, так как нашей новой переменной служила линейная функция вида u=kx+b, но никаких новых букв мы не использовали, а просто применяли свойство VI (Интегралы), а именно:

 Это свойство значительно расширяет таблицу простейших интегралов, так как в силу этого свойства таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией. В занятии 11.1.3. мы учились применять метод подведения переменной под знак дифференциала, используя формулы 1) и 2) (Интегралы), причем, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду:

В примере 1 неявно подразумевалось u=9x-2, что и позволило нам применить свойство VI и формулу 5), в результате чего под знак дифференциала мы подвели (9х-2). Перед знаком интеграла стоит множитель 1/9, так как d (9x-2)=9dx.

1. Рассмотрим пример на применение формулы 4) (Интегралы), а именно, формулы:
2. 
3. 

В примере 2 неявно подразумевается u=25x-1, поэтому, под знак дифференциала подвели 25х-1, отсюда du=25dx. Вот почему перед интегралом стоит множитель 1/25.

Запись имеет метки: непосредственное интегрирование

Источник: https://www.mathematics-repetition.com/11-klass-algebra/11-1-4-neposredstvennoe-integrirovanie.html

Источник: http://student-madi.ru/prochee/vnesenie-pod-znak-differentsiala-s-primerami.html

Применить подведение под знак дифференциала самостоятельно, а затем посмотреть решение

Следующие задачи — общий случай: решаются по определению дифференциала функции:

.

Источник: http://function-x.ru/integral103.html